Variational Inference for Dirichlet Process Priors

Misc.
1

Pyro community, I am working on a multi-task learning problem for classification. I would like to use SVI to learn the model parameters. I am posting it here since the only reference I could find on Dirichlet process was short of answering my questions. I have coded the model part of SVI and have some questions. Below are the details,

Overview

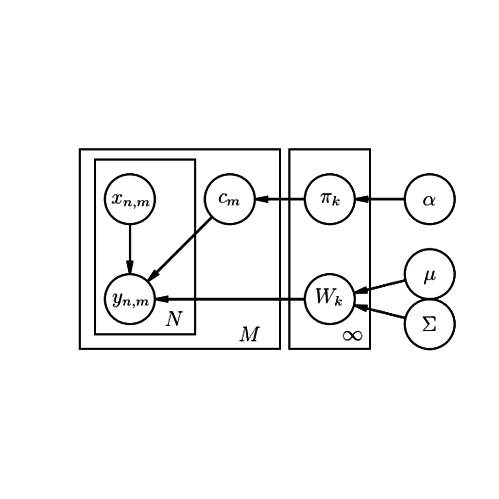
The data generation process is as per the graphical model below.

pgm.png588×588 27.5 KB

At the core I have a classification model, P(Y|X), which uses weights, W, to classify. For now we can assume that this is a binary classification problem e.g., logistic regression. The second part is that there are M (tasks) of these classifiers. Apriori I don’t know the groupings of these M tasks so I would like to infer the groupings as well. A natural parametrization to learn groupings is to put a Dirichlet process prior (parametrized by \pi_k and \alpha) and allow the data to inform us on the number of groups among the M tasks. Here c_m is a categorical variable which is a one-hot encoding of the task groupings.

Pyro Code

Here is code for model part of SVI,

def model(X, Y, tasks):

N, p = X.size()
K = 100
M = len(tasks.unique())

alpha0 = 1.0
crp_tables = []
crp_pi = []
priors = []

# Simple one layer NN with sigmoid activation i.e. logistic regression
nn_model = neural_network_model(p)

for k in range(K):
	crp_pi = torch.Tensor(crp_tables + [alpha0])
	crp_pi /= crp_pi.sum()
	assigned_table = pyro.sample("assigned_table_{}".format(k), dist.Categorical(crp_pi))
	if len(crp_tables) == 0 or assigned_table.item() > len(crp_tables) - 1:
		crp_tables.append(1.0)
	else:
		crp_tables[assigned_table.item()] += 1.0

	# Create unit normal priors over the parameters
	loc = torch.zeros(1, p)
	scale = 2 * torch.ones(1, p)
	w_prior = dist.Normal(loc, scale).independent(1)

	bias_loc = torch.zeros(1)
	bias_scale = 2 * torch.ones(1)
	b_prior = dist.Normal(bias_loc, bias_scale).independent(1)

	priors.append({"linear.weight_{}".format(k): w_prior, "linear.bias_{}".format(k): b_prior})

for m in range(M):
	c_m = pyro.sample("c_{}".format(m), dist.Categorical(crp_pi))

	# lift module parameters to random variables sampled from the priors
	lifted_module = pyro.random_module("module_{}".format(m), nn_model, priors[c_m.item()])

	# sample a neural network (which also samples w and b)
	lifted_reg_model = lifted_module()

	prediction_mean = lifted_reg_model(X[torch.ByteTensor(tasks == m), :].float()).squeeze(-1)

	pyro.sample("obs_{}".format(m), dist.Bernoulli(prediction_mean), obs=Y[torch.ByteTensor(tasks == m)])

Couple of points,

  1. Here X is N x p matrix, Y is N x 1 vector of binary variables and tasks is N x 1 vector of task indicators. For example if M = 3 then tasks will hold entries [0, …, 0, 1, …, 1, 2, …2]

  2. The first for loop is over K groups which simulates the Chinese restaurant process. Inside the same loop I also sample K weights

  3. The second for loop is over M tasks. Here I sample c_m categorical variables from my Dirichlet distribution. Here I also instantiate a one-layer NN with sigmoid activation which is equivalent to logistic regression. This NN code is modified from this Pyro example. The last line treats the observations as sampled from a Bernoulli.

Questions

  1. Does this Model look alright?

  2. I assume there is no better way to do logistic regression in Pyro than via a NN.

  3. I have appended all my weights, W, into a priors list. Is this problematic during inference? Is pyro smart enough to match variables by label names no matter how they are organized.

  4. In my model I would like to learn pi_k (crp_pi in the Model code above) as well. I am not sure how to set this up to be a pyro.sample primitive since it involves the Chinese restaurant process.

  5. Lastly, I am not sure how to set K for Chinese restaurant process when K is independent of my data examples. The right way to do this is to simulate the stick breaking approach using Beta distribution. For now I am not too worried about hard coding K to be 100

Any help is appreciated. I have been at this for two days now.

2 Likes