Hi there! This is my first time using Pyro so I am very excited to see what I can built with it.![]()
Specifically, I am trying to do finite Dirichlet Process clustering with Variational Inference. I want to generalize this into a Chinese Restaurant Process involving an “infinite” number of states. But for now, I am just generating 1-D data from 3 Gaussians with proportions given by a Categorical distribution of a Dirichlet Prior, and we observe each point with a likelihood given by yet another Gaussian.
Basically, the directed graph for the generative process is as follows:
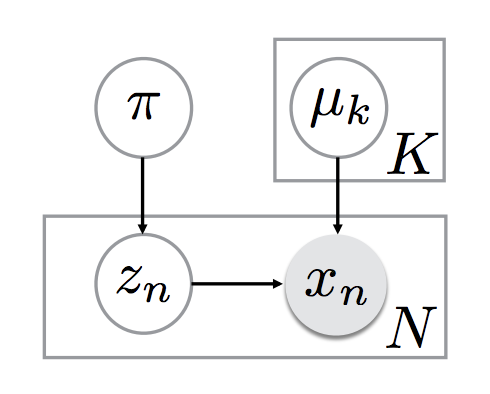
where miu_k indicate the nth mean.
The joint distribution of the same graph is given by this:
Since my joint distribution depends on a global variable(Prior), a cluster-dependent Gaussian, and a likelihood is conditioned on $z_n$s and miu, I am not sure what to do in the model() function. The [SVI_Part II] (SVI Part II: Conditional Independence, Subsampling, and Amortization — Pyro Tutorials 1.8.4 documentation) tutorial has the following code for a similar situation:
def model(data):
beta = pyro.sample("beta", ...) # sample the global RV
for i in pyro.irange("locals", len(data)):
z_i = pyro.sample("z_i", ...)
# compute the parameter used to define the observation
# likelihood using the local random variable
theta_i = compute_something(z_i)
pyro.observe("obs_{}".format(i), dist.mydist,
data[i], theta_i)
But I am still confused as what I should do here. Should I have a nested for-loop inside the main one in which I sample the miu_k independently? To “observe” each data-point given miu_k and z_i, how do I use the normal distribution to give a likelihood?
Here is what I have:
def model(data):
alpha0 = Variable(torch.Tensor([1.0,1.0,1.0]))
prior_mu = Variable(torch.zeros([1, 1]))
prior_sigma = Variable(torch.ones([1, 1]))
for i in range(len(data)):
zn = pyro.observe("latent_proportions", dist.categorical,pi,to_one_hot(y[i].data,3))
mu = pyro.sample("latent_locations", dist.normal,prior_mu,prior_sigma )
# observe data given cluster
for k in range(k):
pyro.sample("latent_locations", dist.normal,prior_mu,prior_sigma )
pyro.observe("obs_{}".format(i), dist.normal,data[i], mu,Variable(torch.ones([1, 1])))
I don really know where to go from here since the last line does not make use of latent_locations(mu) in my formulation. What should I do in this case, when there are two late variables each with a different range in the summation?
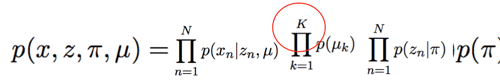

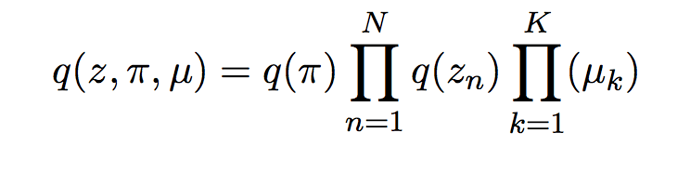
 (we distinguish Categorical distribution and OneHotCategorical distribution, and remove random primitives: dist.normal,… to use
(we distinguish Categorical distribution and OneHotCategorical distribution, and remove random primitives: dist.normal,… to use