Hi! I recently started using numpyro for time series models and am having some problems in using lax.scan functionalities.
In particular, here I am trying to implement a simple state-space model with order-2 autoregressive dynamics, something like:
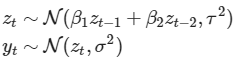 .
.
A vanilla (i.e. without lax.scan) implementation would look something like the following:
def model(T, T_forecast, obs=None):
beta1 = numpyro.sample(name="beta_1", fn=dist.Normal(loc=0., scale=1))
beta2 = numpyro.sample(name="beta_2", fn=dist.Normal(loc=0., scale=1))
tau = numpyro.sample(name="tau", fn=dist.HalfCauchy(scale=1))
sigma = numpyro.sample(name="sigma", fn=dist.HalfCauchy(scale=1))
z_prev1 = numpyro.sample(name="z_1", fn=dist.Normal(loc=0, scale=1))
z_prev2 = numpyro.sample(name="z_2", fn=dist.Normal(loc=0, scale=1))
Z = []
Y = []
for t in range(2, T):
z_t_mean = beta1*z_prev1 + beta2*z_prev2
z_t = numpyro.sample(name="z_%d"%(t+1), fn=dist.Normal(loc=z_t_mean, scale=tau))
Z.append(z_t)
z_prev1 = z_prev2
z_prev2 = z_t
for t in range(T, T+T_forecast):
z_t_mean = beta1*z_prev1 + beta2*z_prev2
z_t = numpyro.sample(name="z_%d"%(t+1), fn=dist.Normal(loc=z_t_mean, scale=tau))
Z.append(z_t)
z_prev1 = z_prev2
z_prev2 = z_t
numpyro.sample(name="y_obs", fn=dist.Normal(loc=np.array(Z[:T-2]), scale=sigma), obs=obs[:T-2])
numpyro.sample(name="y_pred", fn=dist.Normal(loc=np.array(Z[T-2:]), scale=sigma), obs=None)
return Z
where I am trying to be Bayesian over all model parameters (and predictions). This implementation works fine, however, because of the for-loops, this simple model takes way too much time to compile… Following the time-series tutorial on the numpyro documentation I came up with what would seem to me as an equivalent implementation (this time using lax.scan):
def scan_fn(carry, x):
beta1, beta2, z_prev1, z_prev2 = carry
z_t = beta1*z_prev1 + beta2*z_prev2
z_prev1 = z_prev2
z_prev2 = z_t
return (beta1, beta2, z_prev1, z_prev2), z_t
def model(T, T_forecast, obs=None):
beta1 = numpyro.sample(name="beta_1", fn=dist.Normal(loc=0., scale=1))
beta2 = numpyro.sample(name="beta_2", fn=dist.Normal(loc=0., scale=1))
tau = numpyro.sample(name="tau", fn=dist.HalfCauchy(scale=1))
sigma = numpyro.sample(name="sigma", fn=dist.HalfCauchy(scale=1))
z_prev1 = numpyro.sample(name="z_1", fn=dist.Normal(loc=0, scale=1))
z_prev2 = numpyro.sample(name="z_2", fn=dist.Normal(loc=0, scale=1))
_Z_exp = [z_prev1, z_prev2]
__, zs_exp = lax.scan(scan_fn, (beta1, beta2, z_prev1, z_prev2), None, T+T_forecast-2)
Z_exp = jnp.concatenate((jnp.array(_Z_exp), zs_exp), axis=0)
Z = numpyro.sample(name="Z", fn=dist.Normal(loc=Z_exp, scale=tau))
numpyro.sample(name="y_obs", fn=dist.Normal(loc=Z[:T], scale=sigma), obs=obs[:T])
numpyro.sample(name="y_pred", fn=dist.Normal(loc=Z[T:], scale=sigma), obs=None)
return Z_exp
where I use lax.scan to collect the expected values for the latent state z_t. The problem is that when I try running this model, MCMC inference does not converge to meaningful values… Am I missing something evident on how the lax.scan function works or should I implement the model differently?
Thanks!
