Time series modeling in numpyro using MCMC

[chechgm]

Hi all,

I am trying to fit a mutivariate time series model in numpyro. The model is a state-space model with AR(1). The data consists of two time series with missing values. I used the non-centered parametrization and jax.lax.scan as in Using lax.scan for time series in NumPyro. I am doing inference using NUTS. The generative process and the code of the model are the following:

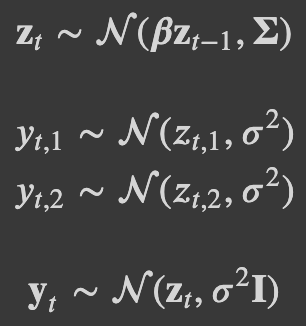
# Definition of the function for the jax.lax.scan
def f(carry, noise_t):
  beta, z_prev = carry
  z_t = beta*z_prev + noise_t
  z_prev = z_t
  return (beta, z_prev), z_t

def model(T, T_forecast, obs1=None, ix_mis1=None, ix_obs1=None, obs2=None, ix_mis2=None, ix_obs2=None):
    """
    Prior for the betas, sigma and first state
    """
    beta = numpyro.sample("beta", numpyro.distributions.Normal(jnp.zeros(2), jnp.ones(2)))
    sigma = numpyro.sample("sigma", numpyro.distributions.HalfCauchy(jnp.ones(2)))
    z_prev = numpyro.sample("z_prev", numpyro.distributions.Normal(jnp.zeros(2), jnp.ones(2)))
    
    """
    Prior for the LKJ including a tau and the sampling noise
    """
    tau = numpyro.sample("tau", numpyro.distributions.HalfCauchy(jnp.ones(2)))
    L_Omega = numpyro.sample("L_Omega", numpyro.distributions.LKJCholesky(dimension=2, concentration=1.))
    Sigma_lower = jnp.matmul(jnp.diag(jnp.sqrt(tau)), L_Omega)
    noises = numpyro.sample("noises", 
                        fn=dist.MultivariateNormal(loc=jnp.zeros(2), scale_tril=Sigma_lower), 
                        sample_shape=(T+T_forecast-1,))
    
    """
    Propagate the dynamics forward using jax.lax.scan
    """
    carry = (beta, z_prev)
    z_collection = [z_prev]

    updated_carry, zs = lax.scan(f=f, init=carry, xs=noises, length=T+T_forecast-1)

    z_collection = jnp.concatenate((jnp.array(z_collection), zs), axis=0)
    
    """
    Sample the observed y (y_obs) and missing y (y_mis)
    """
    y1_obs  = numpyro.sample("y1_obs", numpyro.distributions.Normal(z_collection[ix_obs1, 0], sigma[0]), obs=obs1)
    y1_mis  = numpyro.sample("y1_mis", numpyro.distributions.Normal(z_collection[ix_mis1, 0], sigma[0]))
    y1_pred = numpyro.sample("y1_pred", numpyro.distributions.Normal(z_collection[T:, 0], sigma[0]))

    y2_obs  = numpyro.sample("y2_obs", numpyro.distributions.Normal(z_collection[ix_obs2, 1], sigma[1]), obs=obs2)
    y2_mis  = numpyro.sample("y2_mis", numpyro.distributions.Normal(z_collection[ix_mis2, 1], sigma[1]))
    y2_pred = numpyro.sample("y2_pred", numpyro.distributions.Normal(z_collection[T:, 1], sigma[1]))

I have two questions about the model:

1. Why does the model “learn” a distribution for each of the noises? I would expect the posterior of noises to be just standard gaussians. Almost all of them are, but some are clearly not. If the noise is “exogenous” why can’t I input just numpy samples from a standard gaussian?
2. When I run the model without the predictions (y1_pred and y2_pred) the model runs relatively smoothly (still with the problem in 1) but I get sensible results), but whenever I include the forecasting part the model collapses. That is, the posterior become single values sampled over and over with n_eff=0.5 for all of them.

Thank you,
Sergio

[fehiepsi]

Hi @chechgm, about 1., I guess you want to marginalize the latent variable z? If it is the case, then you might want to use Pyro GaussianHMM instead (currently, that class does not support missing observations - though it is doable).

About 2., you can use Predictive for forecasting. You can distinguish training and forecasting using a flag as in this example. In addition, I think you can remove the missing variables y*_mis because it does not help for inference. If you want to get predictions of those missing values, you can use Predictive after you already get posterior samples using MCMC.

[chechgm]

Thank you for your answer @fehiepsi.

1. About 1 maybe the problem is more conceptual than the programming itself. I think I probably don’t understand the point of reparametrization properly. If I am wrong, the point of reparametrization is to express a distribution in different terms so that the inference is easier. The classical example is N(mu, sigma) vs. mu+sigma*N(0,1). What I find puzzling is that in my program, numpyro is learning mu sigma, but also a posterior for N(0,1). Shouldn’t it “stay” as N(0,1) since the information of the inference is contained in mu and sigma? is this (maybe) a problem of identifiability? Do you have any references on the fundamentals of reparametrization?

2. I think using Predictive makes way more sense than the way it is on the code now. I checked the code you sent, but I think that the flag comes from the fact that you have covariates so it is relatively easy to distinguish between train and forecast. In my case I tried:

y = jnp.empty((T+T_forecast))
y[:T] = numpyro.sample("y", numpyro.distributions.Normal(z_collection[:T], sigma), obs=obs)
y[T:] = numpyro.sample("y", numpyro.distributions.Normal(z_collection[T:], sigma))

which is fairly similar to the code you sent. However I am getting the following error:

TypeError: '<class 'jax.interpreters.xla.DeviceArray'>' object does not support item assignment. JAX arrays are immutable; perhaps you want jax.ops.index_update or jax.ops.index_add instead?

I guess that what I tried is not the way to go. Is there a way around this?

Best,
Sergio

[fehiepsi]

@chechgm Re reparameterization: maybe this Stan reference and this paper are helpful.

numpyro is learning mu sigma, but also a posterior for N(0,1)

NUTS will sample all “latent” variables, including the noises (this is a latent variable in your model, unless you use Kalman filter - like Pyro GaussianHMM distribution - to marginalize it). This is different from the case you use mu and sigma in an “observed” node: NUTS will not sample obs if its declaration is numpyro.sample('obs', dist.Normal(mu, sigma), obs=y).

About predictive, there are many ways to do. You can define an arg forecasting_interval in your model

def model(..., forecasting_interval=0):
    ...
    if forecasting_interval > 0:
        numpyro.sample("y_forecast", dist.Normal(...))

predictive = Predictive(model, posterior_samples)
y_forecast = predictive(PRNGKey(0), ..., forecasting_interval=10)['y_forecast']

For your model, to sample posterior, you set forecasting_interval=0 and only include the observed y*_obs statement. To get posterior predictive, you can set obs* = None. To forecast, you can set forecasting_interval > 0 and sample y*_pred. You can sample y*_mis using either if obs* is None: y_mis = numpyro.sample(...) or if forecasting_interval > 0: y_mis = .... It is pretty flexible to choose which way you want using model args, as long as you don’t mix sample and predictive/forecasting steps.

[chechgm]

@fehiepsi Thank you! I will check the references out!