Hi all!
I am trying to learn NumPyro’s syntax and methods and everything seems very nice and quite intuitive!
I have tried to follow along the book Statistical Rethinking and the very nice examples of fehiepsi.
Now, however, I am trying to apply it to my own data. I have some binomial data where the probability p is a function of the variable z in the following way (we believe): f(z) = p = A(1-q)^(z-1) + c. This function can be be seen as a modified geometric function.
The data is:
N = jnp.array([7642688, 7609177, 8992872, 8679915, 8877887, 8669401])
y = jnp.array([2036195, 745632, 279947, 200865, 106383, 150621])
z = jnp.arange(1, len(N) + 1)
I have tried to fit it using the following model:
def modelA(z, N, y=None):
q = numpyro.sample("q", dist.Beta(7, 3)) # mean = 0.7, shape = 10
A = numpyro.sample("A", dist.Beta(2, 6)) # mean = 0.25, shape = 8
c = numpyro.sample("c", dist.Beta(0.1, 9.9)) # mean = 0.01, shape = 10
fz = numpyro.deterministic("fz", A * (1 - q) ** (z - 1) + c)
numpyro.sample("obs", dist.Binomial(probs=fz, total_count=N), obs=y)
mcmcA = MCMC(NUTS(modelA), num_warmup=1000, num_samples=1000)
mcmcA.run(Key(1), z, N, y)
mcmcA.print_summary()
Which gives some decent results:
sample: 100%|██████████| 2000/2000 [00:08<00:00, 224.93it/s, 7 steps of size 1.86e-01. acc. prob=0.89]
mean std median 5.0% 95.0% n_eff r_hat
A 0.26 0.00 0.26 0.26 0.26 1018.05 1.00
c 0.01 0.00 0.01 0.01 0.01 342.01 1.00
q 0.70 0.00 0.70 0.70 0.70 442.41 1.01
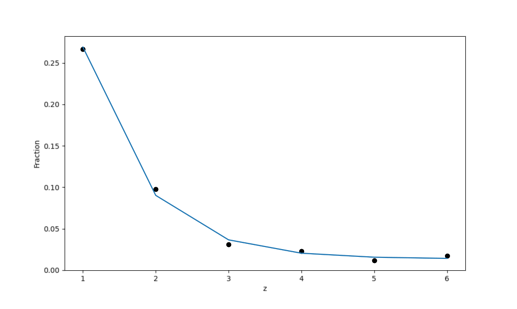
However, when plotting it, one can see that the data is over-dispersed which the model does not account for at all - the variation in the predicted counts is way too small, see e.g. the figure below:
The figure is supposed to show the mean of the predictions and the hpdi which is completely invisible (the standard deviations are about 0.01%).
When reading in Statistical Rethinking about over-dispersion, they recommended using a beta-binomial model instead (see chapter 12), so of course I tried that:
def modelB(z, N, y=None):
q = numpyro.sample("q", dist.Beta(7, 3)) # mean = 0.7, shape = 10
A = numpyro.sample("A", dist.Beta(2, 6)) # mean = 0.25, shape = 8
c = numpyro.sample("c", dist.Beta(0.1, 9.9)) # mean = 0.01, shape = 10
fz = numpyro.deterministic("fz", A * (1 - q) ** (z - 1) + c)
phi = numpyro.sample("phi", dist.Exponential(1))
theta = numpyro.deterministic("theta", phi + 2)
numpyro.sample("obs", dist.BetaBinomial(fz * theta, (1 - fz) * theta, N), obs=y)
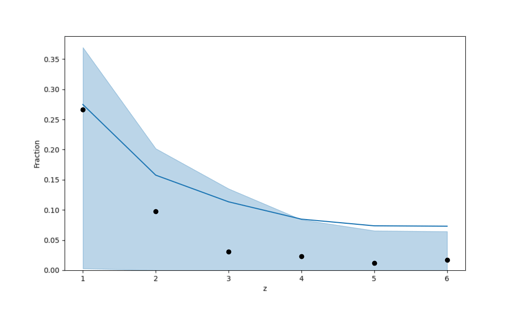
However, with bad results:
mean std median 5.0% 95.0% n_eff r_hat
A 0.20 0.03 0.19 0.16 0.25 4.33 1.17
c 0.07 0.01 0.07 0.05 0.08 5.83 1.00
phi 1.87 0.04 1.86 1.79 1.94 8.66 1.00
q 0.56 0.04 0.57 0.50 0.63 21.56 1.00
It is interesting to look at the plot, because now we can really see the uncertainty in the predictions, yet they completely overshadow any realistic learning (and n_eff is awfully low for all the variables).
What am I missing? Or how do you incorporate the functional form of the probability, f(z), into Numpyro in a working manner?
Thanks a lot and sorry for the long question!
Cheers,
Christian