This is kind of a continuation of an earlier issue I posted a week or two ago, where I was not able to recover the distribution of a latent variable in a simple model of exponential growth. Based on the discussion in that thread, I assumed that Pyro just wasn’t able to do what I was expecting (infer the distribution of a latent variable using observations of a dependent variable), even though it seemed fairly basic.
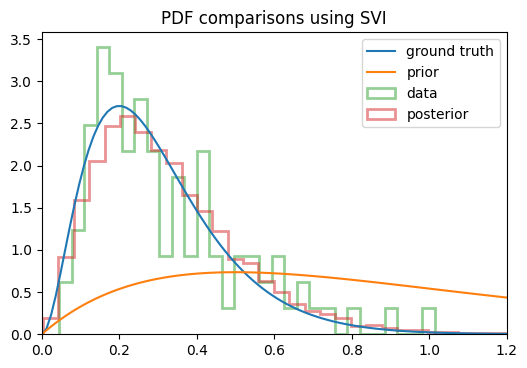
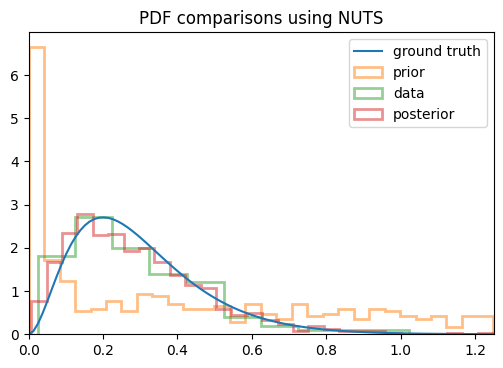
On a whim, I decided to see if MCMC could do it, so I banged out a quick trial with NUTS, and without changing the model/prior at all, I started getting the results I was expecting! You can see below the change in the posterior between using SVI vs NUTS:
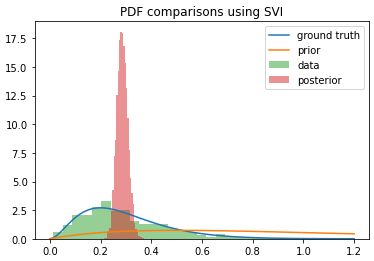
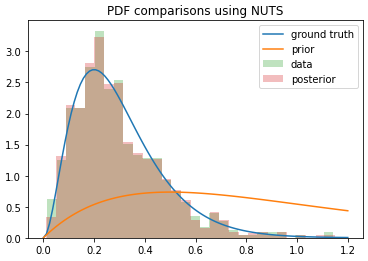
You can see that the posterior I get from SVI converges to the mean of the distribution itself (if I run it for more steps, it keeps getting narrower), whereas NUTS actually returns samples from the posterior as I was hoping. I used the same model in each case, so what’s going on here? Am I using SVI incorrectly?
You can reproduce this with the following code:
import tqdm
import numpy as np
import scipy
import matplotlib.pyplot as plt
import random
import torch
from torch.distributions import constraints as tconst
import pyro
import pyro.distributions as pdist
import pyro.infer
from pyro.infer import MCMC, NUTS, Predictive
import pyro.optim
pyro.enable_validation(True)
####################################################################
## Define model/guide ##
####################################################################
class RegressionModel:
def __init__(self, k, theta):
self.k = torch.tensor(float(k))
self.theta = torch.tensor(float(theta))
# Model used in both SVI and NUTS
def model(self, Y):
for i, y in enumerate(Y):
N = len(y) - 1
noise = 1e-3
with pyro.plate(f"data_{i}", N):
r = pyro.sample(f"r_{i}", pdist.Gamma(self.k, 1/self.theta))
ln_yhat = torch.log(1+r) + torch.log(y[:-1])
pyro.sample(f"obs_{i}", pdist.Normal(ln_yhat, noise), obs=torch.log(y[1:]))
# Guide only used for SVI
def guide(self, Y):
for i, y in enumerate(Y):
N = len(y) - 1
k = pyro.param("k", self.k, constraint=tconst.positive)
theta = pyro.param("theta", self.theta, constraint=tconst.positive)
with pyro.plate(f"data_{i}", N):
r = pyro.sample(f"r_{i}", pdist.Gamma(k, 1/theta))
####################################################################
## Generate data ##
####################################################################
K, THETA = 3e0, 1e-1 # Actual ground truth values
def gen_ts(k, theta, T=10):
y0 = 1
Y = [y0]
for t in range(T):
y0 = (1 + random.gammavariate(k, theta))*y0
Y.append(y0)
return torch.tensor(Y)
# Make a bunch of time series of varying lengths
data = [gen_ts(K, THETA, T) for T in np.random.uniform(1, 10, size=100).round().astype(int)]
####################################################################
## Run SVI ##
####################################################################
pyro.clear_param_store()
model = RegressionModel(2, 0.5)
svi = pyro.infer.SVI(
model=model.model,
guide=model.guide,
optim=pyro.optim.Adam({"lr": 1e-1, "betas": (0.9, 0.9)}),
loss=pyro.infer.Trace_ELBO()
)
num_steps = 200
pbar = tqdm.notebook.tqdm(total=num_steps, mininterval=1)
loss = [] # For tracking loss
ps = pyro.get_param_store()
params = dict() # For tracking variational parameter evolution
alpha = 0.9 # For exponential weighted average of loss
for i in range(num_steps):
loss.append(svi.step(data))
if i == 0 or np.isinf(avg_loss):
avg_loss = loss[-1]
else:
avg_loss = alpha * avg_loss + (1-alpha) * loss[-1]
for k in ps.keys():
try:
params[k].append(ps[k].item())
except KeyError:
params[k] = [ps[k].item()]
pbar.set_description(f"loss={avg_loss: 5.2e}")
pbar.update()
pbar.close()
####################################################################
## Plot posterior from SVI ##
####################################################################
# Ground-truth distribution
x = np.linspace(0, 1.2, 100)
y = scipy.stats.gamma(a=K, scale=THETA).pdf(x)
plt.plot(x, y, label="ground truth")
# Prior distribution
x = np.linspace(0, 1.2, 100)
y = scipy.stats.gamma(a=model.k.item(), scale=model.theta.item()).pdf(x)
plt.plot(x, y, label="prior")
# Data distribution
X = []
for Y in data:
x = ((torch.roll(Y, -1) - Y)/Y).numpy()[:-1]
X.extend(x)
plt.hist(X, bins=30, alpha=0.5, label="sample", density=True)
# The posterior distribution
k = pyro.param('k').item()
theta = pyro.param("theta").item()
x = np.random.gamma(k, theta, size=10000)
plt.hist(x, bins=30, alpha=0.5, label="posterior", density=True)
plt.legend()
plt.title("PDF comparisons using SVI")
plt.show()
####################################################################
## Run NUTS ##
####################################################################
model = RegressionModel(2, 0.5)
nuts_kernel = NUTS(
model.model,
adapt_step_size=True,
adapt_mass_matrix=True,
jit_compile=False,
full_mass=True
)
mcmc = MCMC(
nuts_kernel,
num_samples=20,
warmup_steps=10,
num_chains=1
)
mcmc.run(data)
samples = mcmc.get_samples()
####################################################################
## Plot posterior from NUTS ##
####################################################################
# Ground-truth distribution
x = np.linspace(0, 1.2, 100)
y = scipy.stats.gamma(a=K, scale=THETA).pdf(x)
plt.plot(x, y, label="ground truth")
# Prior distribution
x = np.linspace(0, 1.2, 100)
y = scipy.stats.gamma(a=model.k.item(), scale=model.theta.item()).pdf(x)
plt.plot(x, y, label="prior")
# Data distribution
X = []
for Y in data:
x = ((torch.roll(Y, -1) - Y)/Y).numpy()[:-1]
X.extend(x)
plt.hist(X, bins=30, alpha=0.3, label="data", density=True)
# Posterior samples
samples_flattened = torch.cat([s.flatten() for s in samples.values()]).numpy()
plt.hist(samples_flattened, bins=30, alpha=0.3, label="posterior", density=True)
plt.legend()
plt.title("PDF comparisons using NUTS")
plt.show()