Distribution is converging to the mean

Misc.
6

You know, writing all that made me realize that it is very probable that pyro just can’t handle deterministic relationships - if you write out Bayes’ rule for these kind of relationships, there are delta functions in both the numerator and denominator, which probably kills any attempt to do numerical calculations.

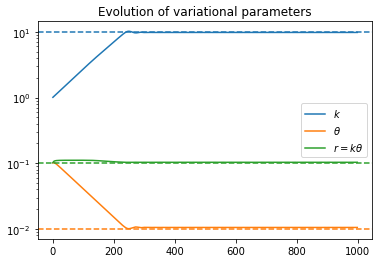
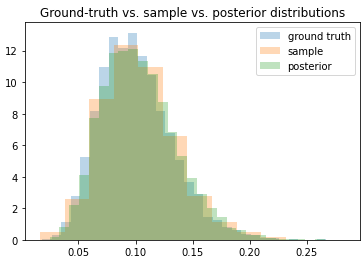
I realized that I could rewrite my problem by rewriting y_{t+1} = (1 + r_t) y_t as r_t = (y_{t+1}/y_t) - 1, and then using that as a direct observation of the distribution for the r’s. Now the variational parameters do converge to their ground truth values, and the distribution matches.

So my model/guide are now

class RegressionModel:
    def __init__(self, mean, std):
        # Convert mean/std into parameters of the gamma dist.
        k = (mean/std)**2
        theta = (std**2)/mean
        self.k = torch.tensor(float(k))
        self.theta = torch.tensor(float(theta))
    
    def model(self, y):
        N = len(y)-1
        k = pyro.param("k", self.k, constraint=tconst.positive)
        theta = pyro.param("theta", self.theta, constraint=tconst.positive)
        with pyro.plate("data", N):
            r = (y[1:]/y[:-1]) - 1
            pyro.sample(f"obs", pdist.Gamma(k, 1/theta), obs=r)
        
    def guide(self, y):
        pass

parameter_evolution

posterior

Thank you for being my rubber duck :slight_smile: