Model can't fit data that requires a large negative bias (intercept)

[bobby]

I’m trying to implement a Bayesian neural network comprising anywhere from zero to two dense layers. In the the simplest case, with zero hidden layers, it’s essentially a linear regression model. The problem is that the model does not fit the training data well. From running a regular linear regression model I know that the bias (intercept) should be around -600, but my model (run without any dense layers) does not get anywhere close. It seems to me that the model gets stuck in a local minimum and can’t get out.

The model itself is loosely based on this blog post: Making Your Neural Network Say “I Don’t Know” — Bayesian NNs using Pyro and PyTorch | by Paras Chopra | Towards Data Science

I’ve read the related post High loss in Ordinary linear regression - #2 by dave but was not able to resolve the issue.

Help would be much appreciated!

class NN(nn.Module):
    '''
    The regression network.
    '''
    def __init__(self, input_size, hidden1_size, hidden2_size, dropout_rate):
        super(NN, self).__init__()
        
        self.input_size = input_size
        self.hidden1_size = hidden1_size
        self.hidden2_size = hidden2_size
        self.dropout = nn.Dropout(p=dropout_rate)
        
        if self.hidden1_size is None and self.hidden2_size is None: 
            self.out = nn.Linear(self.input_size, 1)
        
        elif self.hidden1_size is not None and self.hidden2_size is None:
            self.fc1 = nn.Linear(self.input_size, self.hidden1_size)
            self.out = nn.Linear(self.hidden1_size, 1)
        
        elif self.hidden1_size is None and self.hidden2_size is not None:
            raise ValueError
                    
        elif self.hidden1_size is not None and self.hidden2_size is not None: 
            self.fc1 = nn.Linear(self.input_size, self.hidden1_size)
            self.fc2 = nn.Linear(self.hidden1_size, self.hidden2_size)
            self.out = nn.Linear(self.hidden2_size, 1)
           
 
    def forward(self, x):
        if self.hidden1_size is None and self.hidden2_size is None: 
            x = self.out(x)
            
        elif self.hidden1_size is not None and self.hidden2_size is None:
            x = self.dropout(F.leaky_relu(self.fc1(x)))
            x = self.out(x)
            
        elif self.hidden1_size is not None and self.hidden2_size is not None: 
            x = self.dropout(F.leaky_relu(self.fc1(x)))
            x = self.dropout(F.leaky_relu(self.fc2(x)))
            x = self.out(x)

        return x
    
    
class BayesianRegressor(nn.Module):
    '''
    This PyTorch Module encapsulates the model as well as the
    variational distribution (the guide) for the Regression Model
    '''
    def __init__(self, input_size, hidden1_size, hidden2_size, dropout_rate):
        super().__init__()
        self.df = 100
        
        if hidden1_size is None and hidden2_size is None: 
            self.num_hidden = 0
            
        elif hidden1_size is not None and hidden2_size is None:
            self.num_hidden = 1
            
        elif hidden1_size is None and hidden2_size is not None:
            raise ValueError
            
        elif hidden1_size is not None and hidden2_size is not None: 
            self.num_hidden = 2
        
        # the network
        self.net = NN(input_size, 
                     hidden1_size,
                     hidden2_size, 
                     dropout_rate)
        
        self.softplus = torch.nn.Softplus()
        self.DEVICE = 'cpu'

        
    def model(self, X, y=None, importance=None):

        # set all weights to 1.0 if not provided
        if importance is None:
            importance = torch.ones(X.shape[0])
                
        # set prior for first fully connected layer
        if self.num_hidden in [1, 2]:
            fc1w_prior = Normal(loc=torch.zeros_like(self.net.fc1.weight), 
                                  scale=torch.ones_like(self.net.fc1.weight))
            fc1b_prior = Normal(loc=torch.zeros_like(self.net.fc1.bias), 
                                  scale=torch.ones_like(self.net.fc1.bias))

        # set priopr for second fully connected layer
        if self.num_hidden == 2:
            fc2w_prior = Normal(loc=torch.zeros_like(self.net.fc2.weight), 
                                  scale=torch.ones_like(self.net.fc2.weight))
            fc2b_prior = Normal(loc=torch.zeros_like(self.net.fc2.bias), 
                                  scale=torch.ones_like(self.net.fc2.bias))

        # set the prior for the final layer
        outw_prior =  Normal(loc=torch.zeros_like(self.net.out.weight), 
                            scale=torch.ones_like(self.net.out.weight))
        outb_prior = Normal(loc=torch.zeros_like(self.net.out.bias), 
                            scale=torch.ones_like(self.net.out.bias))
            

        if self.num_hidden == 0:
            priors = {'out.weight': outw_prior, 'out.bias': outb_prior}
        
        elif self.num_hidden == 1:
            priors = {'fc1.weight': fc1w_prior, 'fc1.bias': fc1b_prior,
                      'out.weight': outw_prior, 'out.bias': outb_prior}
            
        elif self.num_hidden == 2:
            priors = {'fc1.weight': fc1w_prior, 'fc1.bias': fc1b_prior,
                      'fc2.weight': fc2w_prior, 'fc2.bias': fc2b_prior,
                      'out.weight': outw_prior, 'out.bias': outb_prior}

        # lift module parameters to random variables sampled from the priors
        lifted_module = pyro.random_module("module", self.net, priors)

        # sample a regressor (which also samples w and b)
        lifted_reg_model = lifted_module()
        
        # make the prediction
        y_hat = lifted_reg_model(X)
        
        # sample the noise magnitude
        sigma = pyro.sample('sigma', dist.LogNormal(loc=0., scale=1.))

        with pyro.poutine.scale(scale=importance):
            pyro.sample("obs", StudentT(df=self.df, loc=y_hat, scale=sigma), obs=y)
        
        return y_hat
    
        
    def guide(self, X, y=None, importance=None):
        
        # First layer weight distribution priors
        if self.num_hidden in [1, 2]:
            fc1w_mu_param = pyro.param("fc1w_mu_param", torch.randn_like(self.net.fc1.weight))
            fc1w_sigma_param = self.softplus(pyro.param("fc1w_sigma_param", torch.randn_like(self.net.fc1.weight)))
            fc1w_prior = Normal(loc=fc1w_mu_param, 
                                  scale=fc1w_sigma_param)

            # First layer bias distribution priors
            fc1b_mu_param = pyro.param("fc1b_mu_param", torch.randn_like(self.net.fc1.bias))
            fc1b_sigma_param = self.softplus(pyro.param("fc1b_sigma_param", torch.randn_like(self.net.fc1.bias)))
            fc1b_prior = Normal(loc=fc1b_mu_param, 
                                  scale=fc1b_sigma_param)
        
        if self.num_hidden == 2:
            # Second layer weight distribution priors
            fc2w_mu_param = pyro.param("fc2w_mu_param", torch.randn_like(self.net.fc2.weight))
            fc2w_sigma_param = self.softplus(pyro.param("fc2w_sigma_param", torch.randn_like(self.net.fc2.weight)))
            fc2w_prior = Normal(loc=fc2w_mu_param, 
                                  scale=fc2w_sigma_param)

            # Second layer bias distribution priors
            fc2b_mu_param = pyro.param("fc2b_mu_param", torch.randn_like(self.net.fc2.bias))
            fc2b_sigma_param = self.softplus(pyro.param("fc2b_sigma_param", torch.randn_like(self.net.fc2.bias)))
            fc2b_prior = Normal(loc=fc2b_mu_param, 
                                  scale=fc2b_sigma_param)

        # Output layer weight distribution priors
        outw_mu_param = pyro.param("outw_mu_param", torch.randn_like(self.net.out.weight))
        outw_sigma_param = self.softplus(pyro.param("outw_sigma_param", torch.randn_like(self.net.out.weight)))
        outw_prior = Normal(loc=outw_mu_param, 
                            scale=outw_sigma_param)

        # Output layer bias distribution priors
        outb_mu_param = pyro.param("outb_mu_param", torch.randn_like(self.net.out.bias))
        outb_sigma_param = self.softplus(pyro.param("outb_sigma_param", torch.randn_like(self.net.out.bias)))
        outb_prior = Normal(loc=outb_mu_param, 
                            scale=outb_sigma_param)
            
        if self.num_hidden == 0:
            priors = {'out.weight': outw_prior, 'out.bias': outb_prior}
        
        elif self.num_hidden == 1:
            priors = {'fc1.weight': fc1w_prior, 'fc1.bias': fc1b_prior,
                      'out.weight': outw_prior, 'out.bias': outb_prior}
            
        elif self.num_hidden == 2:
            priors = {'fc1.weight': fc1w_prior, 'fc1.bias': fc1b_prior,
                      'fc2.weight': fc2w_prior, 'fc2.bias': fc2b_prior,
                      'out.weight': outw_prior, 'out.bias': outb_prior}
        
        # fit the noise
        sigma_mu_param = pyro.param("sigma_mu_param", tensor(0.0))
        sigma_sigma_param = self.softplus(pyro.param("sigma_sigma_param", tensor(1.0)))
        sigma = pyro.sample('sigma', dist.LogNormal(loc=sigma_mu_param, 
                                                    scale=sigma_sigma_param))
        
        lifted_module = pyro.random_module("module", self.net, priors)
        
        return lifted_module()
    
    
    def fit(self, X, y, importance=None, lr=0.01, steps=5000):
        """Fit the model to data.
        """
        self.steps = steps
        
        # put the net into training mode (i.e. turn on drop-out if applicable)
        self.net.train()
        
        # Clear all the parameter store
        pyro.clear_param_store()

        # Define the SVI algorithm.
        my_svi = SVI(model=self.model,
                     guide=self.guide,
                     optim=Adam({"lr": lr}),
                     loss=Trace_ELBO())

        self.train_losses = []
        for i in range(self.steps):

            loss = my_svi.step(X, y, importance) / X.shape[0]

            self.train_losses.append(loss)

            if (i % 100 == 0):
                print(f'iter: {i}, loss: {round(loss, 2)}', end="\r")

                
    def predict(self, X, num_models=50, return_std=False):
        """Predict new samples
        """
        self.net.eval()
        
        predictive = Predictive(model=regressor.model, 
                                guide=regressor.guide, 
                                num_samples=800,
                                return_sites=("obs",))
        
        samples = predictive(X)

        y_hat = samples['obs'].mean(axis=0).detach().numpy()
        sigma = samples['obs'].std(axis=0).detach().numpy()

        if return_std is True:
            return y_hat, sigma
        else:
            return y_hat

Preparing the data:

# dataset from scikit learn
data = sklearn.datasets.load_boston()
Xs = torch.tensor(data['data']).float()
ys = torch.tensor(data['target']).float()

# normalize input
Xs_norm = (Xs - Xs.mean()) / np.sqrt(Xs.var())

# split
Xs_train, Xs_test, ys_train, ys_test, = train_test_split(Xs_norm, ys, 
                                                       shuffle=True,
                                                       test_size=0.2,
                                                       random_state=4321)

Xs_train.shape, Xs_test.shape, len(ys_train), len(ys_test)

Training:

%%time
steps = 5000


regressor = BayesianRegressor(input_size=Xs_train.shape[1], 
                              hidden1_size=None, 
                              hidden2_size=None, 
                              dropout_rate=0.0)

regressor.fit(X=Xs_train, 
              y=ys_train, 
              steps=steps,
              importance=None, 
              lr=0.01)

The bias term is no where near -600

regressor.net.out.bias

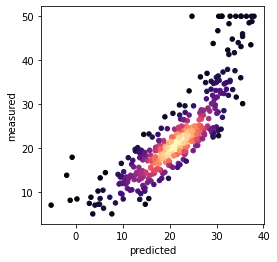
Predicting on the training data, just to show that the model has not fit it:

y_hat, sigma = regressor.predict(Xs_train,
                  num_models=800,
                  return_std=True)

x = y_hat.flatten()
y = ys_train

# Calculate the point density
xy = np.vstack([x,y])
z = scipy.gaussian_kde(xy)(xy)

fig, ax = plt.subplots(figsize=(4,4))
ax.scatter(x, y, c=z, s=20, cmap='magma')
plt.xlabel('predicted')
plt.ylabel('measured')
plt.show()

[martinjankowiak]

@bobby i would generally recommend against implementing a bayesian neural network in raw pyro. a better option would probably be to use TyXe, which is built on top of pyro

[bobby]

@martinjankowiak I take your point. For me, one of the original allures of Pyro was the potential to integrate it with deep learning, but this is proving more difficult than anticipated.

I’m rather new to probabilistic computing, but it seems to me that the models often struggle on data which is handled easily by deterministic algorithms. For instance, the linear model detailed here: Modules in Pyro — Pyro Tutorials 1.8.4 documentation (and outlined in code below) similarly fails on the scikit-learn boston dataset. The model can’t fit the data to get the bias down to -600.

Imports:

import os
import torch
import torch.nn as nn
import pyro
import pyro.distributions as dist
import pyro.poutine as poutine
from torch.distributions import constraints
from pyro.nn import PyroModule, PyroParam, PyroSample
from pyro.nn.module import to_pyro_module_
from pyro.infer import SVI, Trace_ELBO
from pyro.infer.autoguide import AutoNormal
from pyro.optim import Adam

Defining the model:

class BayesianLinear(PyroModule):
    def __init__(self, in_size, out_size):
        super().__init__()
        self.bias = PyroSample(
           prior=dist.LogNormal(0, 1).expand([out_size]).to_event(1))
        self.weight = PyroSample(
           prior=dist.Normal(0, 1).expand([in_size, out_size]).to_event(2))

    def forward(self, input):
        return self.bias + input @ self.weight  # this line samples bias and weight
    
    
class Model(PyroModule):
    def __init__(self, in_size, out_size):
        super().__init__()
        self.linear = BayesianLinear(in_size, out_size)  # this is a PyroModule
        self.obs_scale = PyroSample(dist.LogNormal(0, 1))

    def forward(self, input, output=None):
        obs_loc = self.linear(input)  # this samples linear.bias and linear.weight
        obs_scale = self.obs_scale    # this samples self.obs_scale
        with pyro.plate("instances", len(input)):
            return pyro.sample("obs", dist.Normal(obs_loc, obs_scale).to_event(1),
                               obs=output)

Training:

%%time
smoke_test = False

pyro.clear_param_store()
pyro.set_rng_seed(1)

model = Model(Xs_train.shape[1], 1)
x = Xs_train
y = ys_train

guide = AutoNormal(model)
svi = SVI(model, guide, Adam({"lr": 0.01}), Trace_ELBO())
for step in range(2 if smoke_test else 10001):
    loss = svi.step(x, y) / y.numel()
    if step % 100 == 0:
        print("step {} loss = {:0.4g}".format(step, loss))

Getting the bias:

with poutine.trace() as tr:
    guide(x)
tr.trace.nodes['AutoNormal.locs.linear.bias']['value']

[bobby]

For completeness, here’s the linear model that does succeed.

from sklearn.linear_model import LinearRegression

# train
regressor = LinearRegression()
regressor.fit(Xs_train.numpy(), ys_train.numpy())

# predict
y_hat = regressor.predict(Xs_train.numpy())

# plot
x = y_hat
y = ys_train.numpy()

# Calculate the point density
xy = np.vstack([x,y])
z = gaussian_kde(xy)(xy)

fig, ax = plt.subplots(figsize=(4,4))
ax.scatter(x, y, c=z, s=20, cmap='magma')
plt.xlabel('predicted')
plt.ylabel('measured')
plt.show()

[martinjankowiak]

two points:

• incorporating neural networks into pyro is easy but that sort of approach generally works best in variational autoencoders and the like. bayesian neural networks is a different matter and represents an active area of research where people are still struggling to find scalable inference algorithms that work

• the benefit of scikit learn is that it automates everything. the downside is that it only provides a certain set of models. the upside of pyro is that you can customize models to your heart’s content. the downside is that everything is not automated. in particular there’s no fit method. any dataset that requires giant bias terms probably needs to be standardized (e.g. Y = (Y - Y.mean()) / Y.std()) before it’s fit. scikit learn almost certainly does that for you. pyro does not. for more tips and tricks on the mechanics of fitting models see here

[bobby]

Perhaps I my questions came off the wrong way. I’m not here to complain a bout Pyro. I love the flexibility! I’ve used it to put together a model that is like nothing I’ve seen in sklearn and it’s providing real business value in the setting where I am right now. So yeah, love it!

On the contrary, I was rather frustrated with my own inability to reproduce an outcome that is clearly achievable (as evidenced by the sklearn model). Very happily your tip about y scaling did the trick! The model now almost fits the data as well as the sklean algorithm (as opposed to just fitting the mean of the data as it was doing before). I’m sure I can iron out the last kinks with proper hyperparameter tuning.

Thanks a lot for your help!