I am trying to do a regression on some exponential growth data just as a toy example. My data is generated via y_{t+1} = (1+r_t) y_t, where r_t is sampled from a gamma distribution to enforce positivity (and y_0=1). I can turn this into linear regression by taking the log, so I get a model like \ln(y_{t+1}) = \ln(1+r_t) + \ln(y_t), and although I’ve been able to do normal Bayesian linear regression (following along with the tutorial) where all distributions involved are normally distributed, this one is proving more difficult, perhaps because of some unforeseen quirk of the gamma distribution?
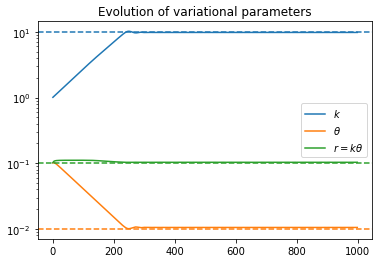
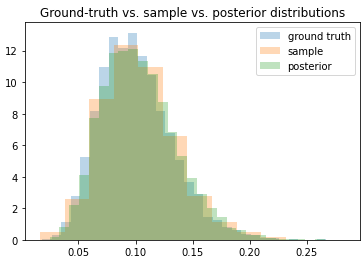
Anyway, the problem I’m having is that when trying to get the posterior for r_t, the density seems to converge toward the correct mean, but the variance keeps shrinking the longer I train. The ELBO loss continues to decrease as though training is proceeding correctly, but the posterior is clearly getting worse as time goes on.
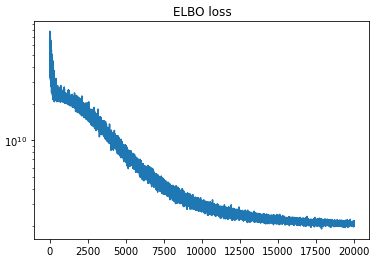
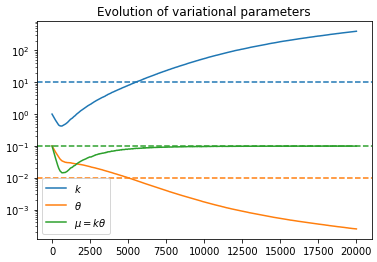
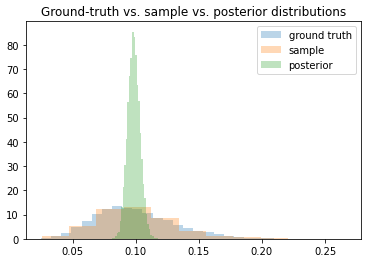
My model is currently set up as below:
import tqdm
import numpy as np
import matplotlib.pyplot as plt
import random
import torch
from torch.distributions import constraints as tconst
import pyro
from pyro.nn import PyroModule, PyroParam, PyroSample
import pyro.distributions as pdist
import pyro.infer
import pyro.optim
class RegressionModel:
def __init__(self, mean, std):
super().__init__()
# Convert mean/std into parameters of the gamma dist.
k = (mean/std)**2
theta = (std**2)/mean
# k and theta will themselves be gamma distributed
self.k_mean = torch.tensor(float(k))
self.k_std = torch.tensor(float(k))
self.theta_mean = torch.tensor(float(theta))
self.theta_std = torch.tensor(float(theta))
self.k_k = (self.k_mean/self.k_std)**2
self.k_theta = (self.k_std**2)/self.k_mean
self.theta_k = (self.theta_mean/self.theta_std)**2
self.theta_theta = (self.theta_std**2)/self.theta_mean
def model(self, y):
N = len(y)-1
sigma = 1e-5
with pyro.plate("data", N):
k = pyro.sample("k", pdist.Gamma(self.k_k, 1/self.k_theta))
theta = pyro.sample("theta", pdist.Gamma(self.theta_k, 1/self.theta_theta))
r = pyro.sample("r", pdist.Gamma(k, 1/theta))
# Need to perform log transform to get additive noise
ln_yhat = torch.log(1+r) + torch.log(y[:-1])
pyro.sample(f"obs", pdist.Normal(ln_yhat, sigma), obs=torch.log(y[1:]))
def guide(self, y):
N = len(y)-1
k_k = pyro.param("k_k", self.k_k, constraint=tconst.positive)
k_theta = pyro.param("k_theta", self.k_theta, constraint=tconst.positive)
theta_k = pyro.param("theta_k", self.theta_k, constraint=tconst.positive)
theta_theta = pyro.param("theta_theta", self.theta_theta, constraint=tconst.positive)
with pyro.plate("data", N):
k = pyro.sample("k", pdist.Gamma(k_k, 1/k_theta))
theta = pyro.sample("theta", pdist.Gamma(theta_k, 1/theta_theta))
r = pyro.sample("r", pdist.Gamma(k, 1/theta))
There is one gamma distribution for the growth rate r, and one gamma distribution each for the hyperparameters k and \theta of the r distribution. The training/fitting procedure is as follows:
## Generate dataset
K, THETA = 10, 0.01
y0 = 1
Y = [y0]
for t in range(500):
y0 = (1 + random.gammavariate(K, THETA))*y0
Y.append(y0)
Y = torch.tensor(Y)
pyro.enable_validation(True)
pyro.clear_param_store()
model = RegressionModel(0.1, 0.1)
svi = pyro.infer.SVI(
model=model.model,
guide=model.guide,
optim=pyro.optim.Adam({"lr": 1e-3, "betas": (0.9, 0.9)}),
loss=pyro.infer.Trace_ELBO()
)
num_steps = 20000
pbar = tqdm.notebook.tqdm(total=num_steps, mininterval=1)
loss = []
ps = pyro.get_param_store()
params = {k: [] for k in ['k_k', 'k_theta', 'theta_k', 'theta_theta']}
alpha = 0.99
for _ in range(num_steps):
loss.append(svi.step(Y))
for k in ps.keys():
params[k].append(ps[k].item())
try:
avg_loss = alpha * avg_loss + (1-alpha) * loss[-1]
except:
avg_loss = loss[-1]
pbar.set_description(f"loss={avg_loss: 5.2e}")
pbar.update()
pbar.close()
Is there something simple that I am overlooking? Or have a made some grave mistake? Is this a known shortcoming of using gamma distributions?