Hi there,
I’m building a model which is related to the scANVI pyro example for modeling count data while learning discrete clusters for data, and I’m having an issue with the parameter fit where the model seems to have a vanishing gradient for fitting zeros. The model is a VAE-GMM which generates values in a latent space z from a gaussian belonging to a discrete cluster, which is decoded linearly by z @ weights + intercept to reconstruct counts with the NB:
class ToyModel(torch.nn.Module):
def __init__(self, n_latent=5, n_var=10, n_components=3):
super(ToyModel, self).__init__()
pyro.clear_param_store()
self.n_latent = n_latent
self.n_var = n_var
self.n_components = n_components
self.scale=1e-4
# FFNNs from antipode
self.encoder = antipode.train_utils.ZLEncoder(num_var=self.n_var, hidden_dims=[1000, 1000, 1000], outputs=[(self.n_latent, None), (self.n_latent, torch.nn.functional.softplus)])
self.classifier = antipode.train_utils.SimpleFFNN(in_dim=self.n_latent, hidden_dims=[1000, 1000, 1000], out_dim=self.n_components)
@config_enumerate
def model(self, data=None):
pyro.module("toy", self)
device = data.device
with poutine.scale(scale=self.scale):
transform_matrix = pyro.sample('transform_matrix_sample', dist.Laplace(torch.zeros(self.n_latent, self.n_var, device=device),100.*torch.ones(self.n_latent, self.n_var, device=device)).to_event(2))
intercept = pyro.sample('intercept_sample', dist.Laplace(torch.zeros(self.n_components, self.n_var, device=device),100.*torch.ones(self.n_components, self.n_var, device=device)).to_event(2))
with pyro.plate('batch', data.shape[0]):
l = data.sum(-1).unsqueeze(-1) + 1.
# Ensure parameters are leaf tensors
locs = pyro.param('locs', 0.1 * torch.randn(self.n_components, self.n_latent, device=device))
scales = pyro.param('scales', torch.ones(self.n_components, self.n_latent, device=device), constraint=constraints.positive)
total_counts = pyro.param('total_counts', 25 * torch.ones(self.n_var, device=device), constraint=constraints.positive)
z = pyro.sample('z', dist.Categorical(logits=torch.ones(self.n_components, device=device)), infer={"enumerate": "parallel"})
latent = pyro.sample('latent', dist.Normal(locs[z], scales[z]).to_event(1))
out_mu = latent @ transform_matrix + intercept[z]
out_mu = torch.nn.functional.log_softmax(out_mu,dim=-1)
if data is not None:
logits = out_mu - total_counts.log() + l.log()
recon = pyro.sample('obs', dist.NegativeBinomial(total_count=total_counts, logits=logits,validate_args=False).to_event(1), obs=data)
def guide(self, data=None):
pyro.module("toy", self)
device = data.device
transform_matrix = pyro.param('transform_matrix', 0.01 * torch.randn(self.n_latent, self.n_var, device=device))
intercept = pyro.param('intercept', 0.01*torch.randn(self.n_components, self.n_var, device=device))
transform_matrix = pyro.sample('transform_matrix_sample', dist.Delta(transform_matrix).to_event(2))
intercept = pyro.sample('intercept_sample', dist.Delta(intercept).to_event(2))
with poutine.scale(scale=self.scale):
with pyro.plate('batch', data.shape[0]):
locs_mu, locs_std = self.encoder(data)
latent = pyro.sample('latent', dist.Normal(locs_mu, locs_std).to_event(1))
weights_probs = pyro.sample('z', dist.Categorical(logits=self.classifier(latent)), infer={"enumerate": "parallel"})
Here I have generated a synthetic dataset of counts from clusters, and compared it to the reconstructed values learned by the model. The model does an okay job reconstructing the true clusters:
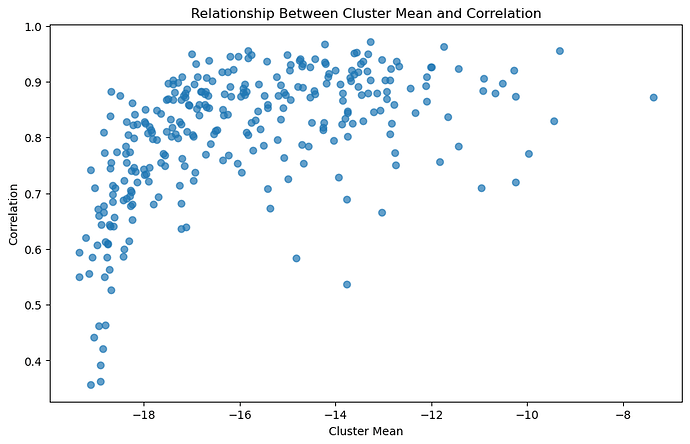
The issue that I’m finding is that the model ‘pays more attention’ to high mean variables, while ‘ignoring’ low mean variables, especially those whose true value is 0. Looking at the correlation of variables with low means compared to high means (the values are very low because they’re logsoftmax’ed):
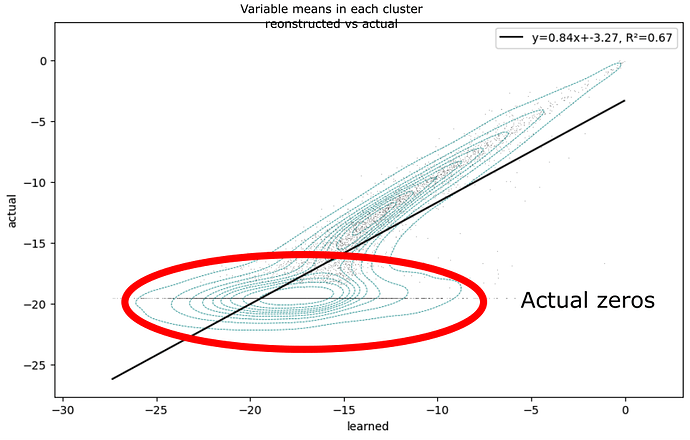
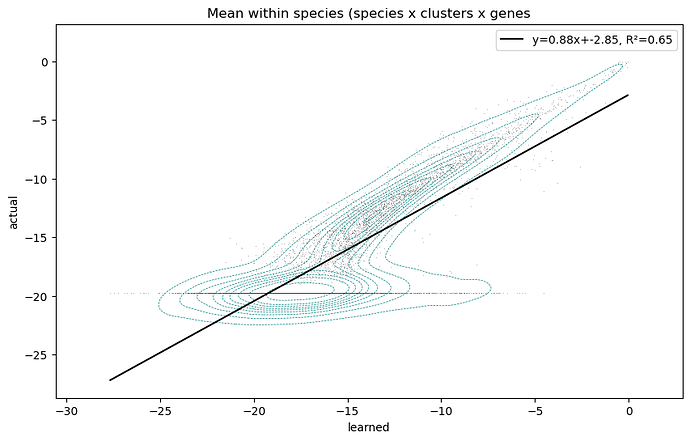
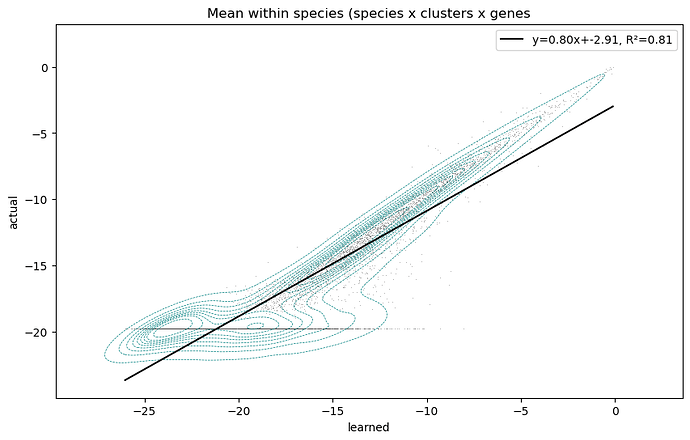
Then when I look at the fit vs actual for each cluster mean for every variable, it’s clear that the model struggles to reconstruct low-mean variables, and often ignores true zeros:
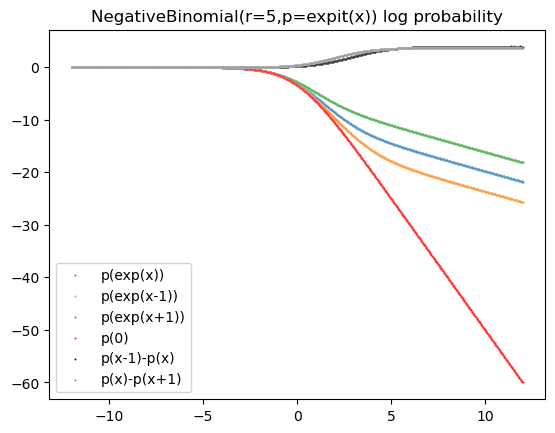
My goal is to have all the variables fit with equal precision, however it clearly is not. I suspect the problem is related to a vanishing gradient in the negative binomial distribution log_probability for low values.
My question is: Is there a way to tweak this model so that I get a parsimonious fit of the parameters, while also being more confident that they are reconstructing the true values with equal accuracy? I’ve tried many things, using LogNormal, adding a Bernoulli for observed zeros, scaling etc. I’ve been stuck on this problem for months and honestly if you come up with the solution that solves my problem in the real model (needs to maintain laplace priors etc so parameters can be interpreted as having equal scale), I’d happily acknowledge you in the manuscript for this method (or grant you any wish).
Thanks so much!
P.S. You can find the full notebook with code to run this model, as well the repo containing the full model (designed to model cell type evolution across species). scANTIPODE/examples/improve_fit/Toy-LogSoftmax-NB-WithLaplacePriors-InitRandn.ipynb at main · mtvector/scANTIPODE · GitHub