ValueError: Guide Producing NaNs

perceptron · October 19, 2022, 5:58pm

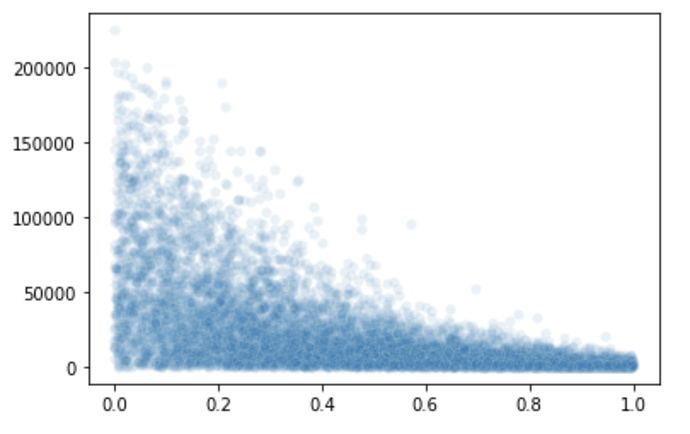
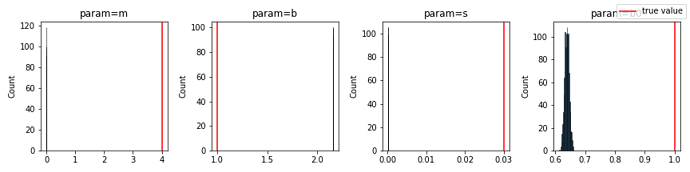
My goal is to learn the relationship between a variable and the second parameter of a beta distribution. SVI fails with a ValueError stemming from NaNs in the MultivariateNormal guide.

Minimal Example:

# model definition
def model5(ac=None, c=None, N=None):
    b0 = sample('b0', LogNormal(0., 0.1).to_event())
    
    m = sample('m', Normal(1., 2.).to_event())  # slope
    b = sample('b', Normal(1., 1.).to_event())  # intercept
    b1_scale = sample('s', Exponential(1.))
    
    N = N if N is not None else 20
    with plate("data", N, dim=-1):  
        c = sample('c', Uniform(0., 1.), obs=c)  # independent variable
        b1_loc = m * c + b  # linear function
        b1 = sample('b1', LogNormal(b1_loc, b1_scale))
        ac = sample('ac', BetaBinomial(b0, b1, total_count=252_000), obs=ac)
        return ac, c

print(model5(N=5))
print_shapes(model5)
sns.scatterplot(x=res[1], y=res[0], alpha=0.1)

# condition and sample the model
conditioned_model = pyro.poutine.condition(model5, data={'b': 1., 'm': 4})
res = conditioned_model(N=10000)

# SVI with multivariate normal guide
train_model(model5, obs=[res[0], res[1], 10000])

Outputs:

(tensor([  1827.,  45182., 186284., 250143., 248686.]),
 tensor([0.2874, 0.8567, 0.2700, 0.5788, 0.7854]))

Trace Shapes:     
 Param Sites:     
Sample Sites:     
      b0 dist    |
        value    |
     log_prob    |
       m dist    |
        value    |
     log_prob    |
       b dist    |
        value    |
     log_prob    |
       s dist    |
        value    |
     log_prob    |
    data dist    |
        value 20 |
     log_prob    |
       c dist 20 |
        value 20 |
     log_prob 20 |
      b1 dist 20 |
        value 20 |
     log_prob 20 |
      ac dist 20 |
        value 20 |
     log_prob 20 |


Elbo loss: 120314.78125
---------------------------------------------------------------------------
ValueError                                Traceback (most recent call last)
File ~/Library/Caches/pypoetry/virtualenvs/statistical-rethinking-64KwZK9C-py3.9/lib/python3.9/site-packages/pyro/poutine/trace_messenger.py:174, in TraceHandler.__call__(self, *args, **kwargs)
    173 try:
--> 174     ret = self.fn(*args, **kwargs)
    175 except (ValueError, RuntimeError) as e:
...
...
...
ValueError: Expected parameter loc (Tensor of shape (10004,)) of distribution MultivariateNormal(loc: torch.Size([10004]), scale_tril: torch.Size([10004, 10004])) to satisfy the constraint IndependentConstraint(Real(), 1), but found invalid values:
tensor([   nan,    nan,    nan,  ..., 2.3503, 2.1330, 1.2780],
       grad_fn=<ExpandBackward0>)
                    Trace Shapes:            
                     Param Sites:            
     AutoMultivariateNormal.scale       10004
AutoMultivariateNormal.scale_tril 10004 10004
       AutoMultivariateNormal.loc       10004
                    Sample Sites:            
                    Trace Shapes:            
                     Param Sites:            
     AutoMultivariateNormal.scale       10004
AutoMultivariateNormal.scale_tril 10004 10004
       AutoMultivariateNormal.loc       10004
                    Sample Sites:

I saw another forum post with a similar issue. The OP stated that setting all parameters to torch.float64 solved his/her issue. That does not work for me. Happy to provide that code if it helps.

martinjankowiak · October 20, 2022, 5:00pm

please refer to this tutorial for some tips. in particular take a look at tips #1, #7 (see init_scale) and #10

perceptron · October 20, 2022, 9:11pm

Thanks for the direction, @martinjankowiak.

Decreasing the learning rate does indeed seem to prevent the very negative ELBO loss and the ValueError due to NaNs from the guide!

However, SVI seems to be doing a really poor job of approximating known parameters from my synthetic dataset:

Here is my code for reference:

# model for generating dummy data
def model5_gen(ac=None, c=None, N=None):
    b0 = 1. 
    m = 4. # slope
    b = 1. # intercept
    b1_scale = 0.03
    
    N = N if N is not None else 20
    with plate("data", N, dim=-1):  
        c = sample('c', Uniform(0., 1.), obs=c)  # independent variable
        b1_loc = m * c + b  # linear function
        b1 = sample('b1', LogNormal(b1_loc, b1_scale))
        ac = sample('ac', BetaBinomial(b0, b1, total_count=252_000), obs=ac)
        return ac, c

# dummy data
res = model5_gen(N=5000)

# svi 
pyro.clear_param_store()
mv_guide = pyro.infer.autoguide.AutoMultivariateNormal(model5_batch, init_scale=0.01)
adam = pyro.optim.Adam({"lr": 0.001}) 
elbo = pyro.infer.Trace_ELBO()
svi = pyro.infer.SVI(model5_batch, mv_guide, adam, elbo)
enumerated = True
losses = []
for step in tqdm(range(15000)):
    loss = svi.step(res[0], res[1], 5_000)
    losses.append(loss)
    if step % 100 == 0:
        print("Elbo loss: {}".format(loss))

# sample the posterior
with plate('post', 1000, dim=-2):
    post_samples = mv_guide()
    
f, axs = plt.subplots(1,4, figsize=(12,3))
sns.histplot(post_samples['m'].squeeze().detach(), ax=axs[0])
axs[0].axvline(4., color='red')
axs[0].set_title('m')
sns.histplot(post_samples['b'].squeeze().detach(), ax=axs[1])
axs[1].axvline(1., color='red')
axs[1].set_title('b')
sns.histplot(post_samples['s'].squeeze().detach(), ax=axs[2])
axs[2].axvline(.03, color='red')
axs[2].set_title('s')
sns.histplot(post_samples['b0'].squeeze().detach(), ax=axs[3])
axs[3].axvline(1., color='red')
axs[3].set_title('b0')

Do you see anything I’m doing glaringly wrong? Is there something about the model that makes this learning task impossible?
Thanks again for your advice.

martinjankowiak · October 20, 2022, 10:20pm

what’s an?

perceptron · October 20, 2022, 11:26pm

For the sake of this example, an is just a constant = 252_000.

martinjankowiak · October 23, 2022, 5:12pm

i’m not sure what’s going on: i think your model is just weird.

the betabinomial already has “noise” injected into it via the beta distribution so i’m not sure why you are injecting additional noise with a lognormal distribution. the prior over c seems a bit strange as well. also normally i’d expect that you parameterize the mean of the betabinomial (which is given as a particular ratio of the concentrations) and not the second concentration parameter directly

fritzo · October 28, 2022, 3:32pm

I second @martinjankowiak’s observation that BetaBinomial + LogNormal noise is probably too-overdispersed. I used to start with overdispersed distributions, but after getting burned a few times I now try to start with simple Binomial models, then optionally either switch to BetaBinomial or add a LogNormal parameter in the hierarchy, but the overdispersion is really a second step once you’ve gotten the simple model working.

perceptron · October 28, 2022, 8:32pm

Removing the additional noise from the LogNormal did seem to fix the problem!

For anyone finding this thread in the future, here is a version of the model that works:

@config_enumerate
def model3_batch(ac=None, an=None, g=None, c=None,  l=None, N=None):
    b0 = sample('b0', LogNormal(zeros(num_genes,), ones(num_genes,)).to_event())
    m = sample('m', Normal(ones(2,)*-60., ones(2,)*10).to_event())
    b = sample('b', Uniform(zeros(2,), ones(2,)*200).to_event())
    N = 1000 if N is None else N
    with plate('data', N, subsample_size=1000, dim=-1) as ind:
        
        c_obs = c[ind] if c is not None else None
        l_obs = l[ind] if l is not None else None
        ac_obs = ac[ind] if l is not None else None
        an_obs = an[ind] if an is not None else 251000
        g_obs = g[ind] if g is not None else None
        
        g = sample('g', Categorical(probs=ones(100,)), obs=g_obs).long()
        c = sample('c', Uniform(0., 1.), obs=c_obs)
        l = sample('l', Bernoulli(probs=0.5), obs=l_obs, infer={'enumerate': 'parallel'}).long()
        b1 = m[l] * c + b[l]
        b1 = torch.clamp(b1, min=1.)
        ac = sample('ac', BetaBinomial(b0[g], b1, total_count=an_obs), obs=ac_obs)
        return b1

The torch.clamp seems a bit inelegant, but the model fitting check seems to capture the true parameters pretty well, so I don’t think it’s getting in the way of the SVI.
I do have some confusion about discrete inference with this model. Ideally I’d like to quantify the uncertainty in the assignment of the ‘l’ site in the conditioned posterior. However, at the moment I am stuck sampling the posterior many times with temperature=1 and taking the mean assignment (a point estimate). I suspect there is a better way to do this.
I do realize this is tangential to the original issue, so I can start another thread for this to keep things organized.