Using numpyro.factor() in an SVI guide

[Hourglass]

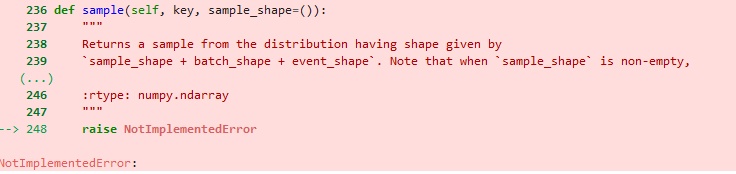
I am playing with some basic implementations of SVI in NumPyro, and having issues getting my guide’s to work for all but the most basic of dummy distributions. The simple example I’ve been working with is using SVI to recover a two-variable gaussian distribution. I have seen people use numpyro.factor() in other posts on this forum, so I know this should be a workable approach, but I am not getting consistent results. E.g. for the models:

def model_factor():
    '''Gaussian distribution using factor()'''
    x = numpyro.sample('x', dist.Uniform( -10 , 10))
    y = numpyro.sample('y', dist.Uniform( -10 , 10))

    log_fac = -1/2 * ( (x/sig1)**2 + (y/sig2)**2 )
    log_fac -= jnp.log(sig1*sig2)
    numpyro.factor('logfac', log_fac)


def model_nofactor():
    '''Gaussian without using factor()'''
    x = numpyro.sample('x', dist.Normal( 0 , sig1))
    y = numpyro.sample('y', dist.Normal( 0 , sig2))

And the guides:

def guide_factor():
    '''Gaussian guide using factor()'''
    sig1_q = numpyro.param('sig1_q', 2.0, constraint = constraints.positive)
    sig2_q = numpyro.param('sig2_q', 2.0, constraint = constraints.positive)

    x = numpyro.sample('x', dist.Uniform( -10 , 10))
    y = numpyro.sample('y', dist.Uniform( -10 , 10))

    log_fac  = -1/2 * ( (x/sig1)**2 + (y/sig2)**2 )
    log_fac -= jnp.log(sig1*sig2)
    numpyro.factor('log_fac', log_fac)


def guide_nofactor():
    '''Gaussian guide  without using factor()'''
    sig1_q = numpyro.param('sig1_q', 1.0, constraint = constraints.positive)
    sig2_q = numpyro.param('sig2_q', 1.0, constraint = constraints.positive)

    x = numpyro.sample('x', dist.Normal( 0 , sig1_q))
    y = numpyro.sample('y', dist.Normal( 0 , sig2_q))

I recover the correct results for sig_1 and sig_2 when using guide_nofactor, but not guide_factor, even though the probabilistic modelling is equivalent.

In case it ends up being relevant, I am calling them like:

svi_FF = SVI(model_factor, guide_factor, optimizer, loss=Trace_ELBO())
svi_FN = SVI(model_factor, guide_nofactor, optimizer, loss=Trace_ELBO())
svi_NF = SVI(model_nofactor, guide_factor, optimizer, loss=Trace_ELBO())
svi_NN = SVI(model_nofactor, guide_nofactor, optimizer, loss=Trace_ELBO())

#-------------------------------------------------------------------------
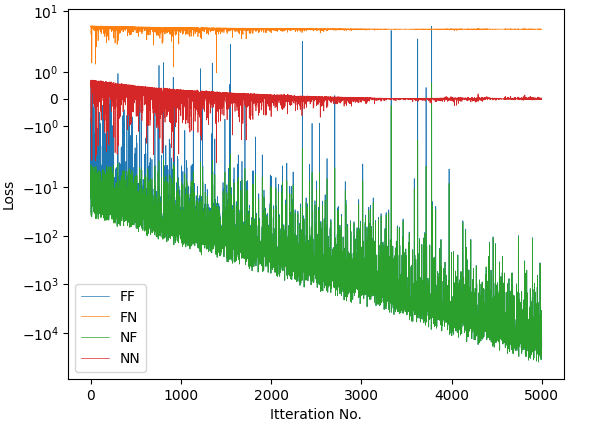
for svi, label in zip([svi_FF, svi_FN, svi_NF , svi_NN ], ["FF", "FN", "NF", "NN"]):
    svi_result = svi.run(random.PRNGKey(1), 5000)
    print(label)
    for key, val in zip(svi_result.params.keys(), svi_result.params.values()):
        print("%s:\t%0.3f" %(key,val) )

And am getting outputs that are consistent between models, but not guides. I’ve tried different tweaks to the log factor in guide_factor(), but similarly poor results.

FF
sig1_q:	0.715
sig2_q:	0.714


FN
sig1_q:	1.025
sig2_q:	1.994


NF
sig1_q:	0.715
sig2_q:	0.714


NN
sig1_q:	1.025
sig2_q:	1.994

[martinjankowiak]

this is wrong

jnp.log(jnp.sqrt(sig1*sig2))

it should be jnp.log(sig1 * sig2) (no sqrt)

[Hourglass]

I’ve included that for completeness, as the normalizing constant shouldn’t matter. I’ve edited my post / code for accuracy, but outputs have not changed. Again, the two models are consistent / correct, it’s only the guide_factor() that isn’t performing properly.

In case it helps in anyway, Ive also got a log-plot of the loss during the svi run for each model / guide pairing:

[martinjankowiak]

i’m not sure if using a uniform distribution like that is a great idea. try ImproperUniform, something like

from numpyro.distributions import ImproperUniform, constraints
x = sample('x', ImproperUniform(constraints.real, ()))

[Hourglass]

Replacing:

dist.Uniform(-10,10)

With:

ImproperUniform(constraints.real, (), event_shape=() )

Yields no issues in model_factor(), but, when used in guide_factor(), gives rise to a large error ending with the following:

I am not too familiar with improper distributions, so please excuse me if I’ve made an obvious mistake somewhere.

[martinjankowiak]

sorry i wasn’t thinking very clearly when i first read this. you can’t use guide_factor like that in SVI. your factor-based model should work in HMC (since that only depends on the log density and its gradient) but SVI requires a (parameterized) guide sampler. irrespective of what factors you put in the guide, your guide says that x and y should be sampled from a fixed uniform distribution. it is of course ok to use factor statements in a guide, but they should be understood as terms that get added to the ELBO objective. you cannot simulate a gaussian sampler the way you are attempting to do so in guide_factor.

[Hourglass]

Ah okay, so the factor() term is added to the ELBO rather than the likelihood of the dummy model. Is there a way to fit an arbitrary parameterized likelihood function with SVI? In cases even as simple as a multivariate gaussian, things seem to rapidly get out of hand unless using an autoguide.

[martinjankowiak]

can you specify what you mean exactly?

a guide needs to be composed of primitive samplers like Normal, Dirichlet, etc

[Hourglass]

As a simple example, I might have some arbitrary distribution p(x,y), otherwise solvable via HMC or MCMC, that I want to approximate with a dummy function q(x,y|\phi) that is made out of primitive sampler ‘building blocks’ but in a non trival way, e.g. a multimodal gaussian and cauchy distribution rotated by some angle:

So I want to build a guide for a dummy function of the form:

q(x,y | b, \theta) = [e^{-(u_1-b)^2} + e^{-(u_1+b)^2}]\cdot \frac{1}{1+u_2^2}

Where:

u_1 = cos(\theta) x - sin(\theta) y, \;\;\; u_2 = cos(\theta) x + sin(\theta) y

We have an objective function in the form of the KL divergence / ELBO, which we can minimize / maximize as a function of our dummy model parameters \phi=\{b,\theta\}:

KL(b,\theta) = \iint q(x,y|b,\theta)\cdot ln\left| \frac{p(x,y)}{q(x,y|b,\theta)} \right| dx dy

SVI seems like the correct job for this, but I’m struggling to find the shortest path to constructing a guide that properly describes q(x,y | b, \theta). I’m only concerned with relatively simple continuous domain cases, but I’m not clear on how to compose simple distributions (Normal, Uniform, Cauchy etc) into arbitrary likelihood functions within the guide.

What is the best practice / shortest path to constructing a guide that will allow me to perform SVI on this distribution for an arbitrary model p(x,y)?

[martinjankowiak]

the thing is that vanilla svi expects a normalized guide distribution. your ansatz for q is presumably not normalized. your best bet would be to see if something like q(x,y) can be obtained from some invertible transformations applied to some known normalized distribution composed of basic primitives like Normal

[martinjankowiak]

actually you already have that since in that form your distribution is a product of a mixture of 2 gaussian distribution and a cauchy distribution

[Hourglass]

Could you explain / direct me to an example of how to construct a guide of that sort of form? I.e. how to mix / reparameterize base distributions?

[martinjankowiak]

you should be able to do something like

u1 = numpyro.sample("u1", MixtureSameFamily(...))
u2 = numpyro.sample("u2", Cauchy(...))

x = numpyro.deterministic("x", solve_for_x_in_terms_of_u1_u2(u1, u2))
y = numpyro.deterministic("y", solve_for_y_in_terms_of_u1_u2(u1, u2))

doc links:

• cauchy
• mixutre

[Hourglass]

If I define ‘x’ and ‘y’ in terms of numpyro.deterministic() in the guide, I get an error stating that “Site x must be sampled in trace.”. Is there some additional step I’m missing here? I can get the right results if I instead use x = sample("x", dist.Delta(x(u1,u2))). Is this good practice?

[martinjankowiak]

oh whoops that’s actually what i meant => use Delta