Using detached sample values within the model

[Rajitha]

Hello

I have been using numpyro for quite some time and find it very useful!

Recently I tried to implement a model which has 2 obs sites: 1) a fixed observed input and 2) a random variable.

A simplified version of the model is as below:

log (y_train) ~ N(a+b*log(h_train), e)

I have a set of y_train and h_train from which I want to learn the parameters a, b and e

Then I want to draw a new y_star conditional on a[j], b[j], e[j] and h_star. [j] represent each iteration in the mcmc chain. I am using NUTS sampler

Next I model the y_star using a set of x_inputs

y_star ~ Gamma(mu,sig)

mu = x_input * beta
sig = x_input * phi

The goal is to learn a, b, e, beta and phi all together.

I tried to used numpyro.param('a_j',a) to detach it from the log_prob calculation in the second observed statement but I realized that it only returns the initial_value, and not the value ‘a’ takes in each iteration.

My implementation is given below:

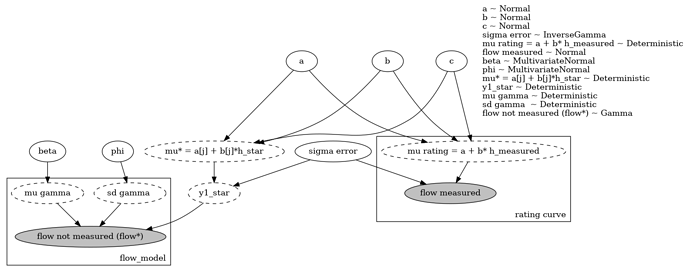
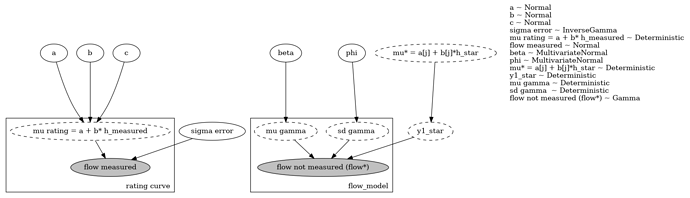
def full_model_single(y1_rating,h1_rating,x,h1_star):
    n_train = len(y1_rating)
    n = x.shape[1]

    #Rating curve parameters
    a = numpyro.sample('a', dist.Normal(0,n_train*10))
    b = numpyro.sample('b', dist.Normal(0,n_train*10))

    sigma2 = numpyro.sample('sigma error', dist.InverseGamma(1,2))

    with numpyro.plate('rating curve',n_train):
        mu = numpyro.deterministic('mu rating = a + b* h_measured', a + b*h1_rating)
        numpyro.sample('flow measured', dist.Normal(mu, sigma2), obs=y1_rating)

    # Fixing them to the values drawn
    # But I realized this is wrong

    a_j = numpyro.param('a_j', a)
    b_j = numpyro.param('b_j', b)
    sigma2_j = numpyro.param('sigma2_j', sigma2)


    #Flow model parameters
    beta = numpyro.sample('beta',dist.MultivariateNormal(jnp.zeros(3),covariance_matrix = n*jnp.eye(3)))
    phi = numpyro.sample('phi',dist.MultivariateNormal(jnp.zeros(3),covariance_matrix = n*jnp.eye(3)))

    mu_star = numpyro.deterministic('mu* = a[j] + b[j]*h_star', a_j + (b_j*h1_star) )

    #Draw a y_star using the sampled a, b and sigma
    y1_log_star = dist.Normal(mu_star ,sigma2_j).sample(rng_key_)
    y1_star = numpyro.deterministic('y1_star', jnp.exp(y1_log_star))
    
    with numpyro.plate('flow model',n):
      mean = numpyro.deterministic('mu gamma', jnp.exp(x.T @ beta))
      sd = numpyro.deterministic('sd gamma ', jnp.exp(x.T @ phi))
      numpyro.sample("flow not measured (flow*)", dist.Gamma(mean**2/sd**2,rate=mean/sd**2), obs=y1_star)

This application is in hydrology where ‘h’ is measured height of flow at a station and ‘y’ is the volume of streamflow discharge.

Any help or leads would be very much appreciated!

Cheers
Rajitha

[fehiepsi]

Edit: maybe I misunderstand your question. the following approach detaches value before computing log probability. If you only need to detach, you can use stop_gradient.

A trick that you can do is to define:

class DetachNormal(dist.Normal):
    def log_prob(self, value):
        return super().log_prob(stop_gradient(value))

def model(...):
    a = numpyro.sample('a', dist.DetachNormal(0, n_train * 10))
    a = stop_gradient(a)

You can also use the StopGradient distribution in coix.

[Rajitha]

Thank you @fahiepsi

May be I was not very clear with the question.

My model has two parts:

1. rating curve (parameters: a, b and sigma2)
2. flow model (parameters: beta, phi)

The metropolis sampling equivalent should look like this:

for i in range(iterations):

1. Draw a[i], b[i], sigma2[i] from p(a,b,sigma2|y_train,h_train)
2. Draw y_star[j] from p(y_star |a[j],b[j], sigma2[j], h_star)
3. Draw beta[j] and phi[j] from p(beta[j], phi[j] |y_star[j],x_input)

First I draw samples from the posterior for a, b and sigma2, from the rating curve part, lets say a[j], b[j] and sigma2[j] from p(a,b,sigma2|y_train,h_train)

Once these samples are drawn, I want a ‘copy’ of it, say ‘a_j’ which is now not a ‘random variable’ to generate y_strar at each iteration, from p(y_star|a[j],b[j],sigma2[j],h_star).

If I do not detach a, b and sigma2, the graph of the model will look like this which is not correct (mu* is independent of a, b and sigma2 conditional on a[j],b[j] and sigma2[j] ):

Instead I want this:

Any potential tips and tricks would be appreciated

[martinjankowiak]

can you contextualize further what you’re doing? if i understand it right you’re doing something non-bayesian. in particular you want information to flow from A to B but not from B to A. is that right? if so it may be a bit awkward to shove into numpyro, since it doesn’t appear to represent a bayesian inference problem

[Rajitha]

Hi Martin

A bit of context, in hydrology, we only measure the ‘height of the water level’ to estimate ‘streamflow volume’. Since measuring ‘volume’ is expensive, usually they measure ‘height’ and ‘volume’ for a few days and build up a relationship between ‘height’ and ‘volume’ for each station.

We assume this volume - height relationship to be of the form:

log(volume) = a + b* log(height) + error

My goal is to first:

1. Learn this relationship between ‘height: h’ and ‘volume: y’. That is sampling ‘a’, ‘b’ and ‘sigma2’ in my model.

2. Then, for another set of days which I have only ‘height: h_star’ measurements, I draw ‘volume: y_star’ conditional on the learned ‘a’, b’ and ‘sigma2’ and ‘h_star’

3. Now for this ‘volume: y_star’, I have a model of the form:
   y_star ~ Gamma(mu,sig);

where;
mu = x_input * beta
sig: x_input * phi

The goal is to use the learned values of beta and phi to predict ‘volume’ using ‘x_input’ where x_input: rainfall, temperature.

[Rajitha]

It is a fully Bayesian model but rather the issue here is about setting independence I believe (as we see in the model graph)

You are absolutely spot on about information flowing from A to B but not from B to A, if we consider my ‘rating curve’ model as A and ‘flow model’ as B.

Thank you for your response, let me know if you have any suggestions.

[martinjankowiak]

if i understand you right i don’t see why you can’t write your model in the generic form

def model(...):
    numpyro.sample(.... prior terms ...)
    y_star = numpyro.sample("y_star", ... depends on a/b/sigma2/h_star... )  # this introduces is a latent variable
    numpyro.sample("y_star_obs", ... depends on mu/sig..., obs=y_star). # we observe y_star using latent mu/sig

note you shouldn’t use expressions like this in the model:

dist.Normal(mu_star ,sigma2_j).sample(rng_key_)

instead follow the syntax in the tutorials which combines a series of sample statments (observed or latent) and deterministic computations in between. if you’re doing vanilla bayesian modeling there should be no need to introduce rng keys into your model.