Dear expert,
From the class below
class MixtureModel_jax():
def __init__(self, locs, scales, weights, *args, **kwargs):
super().__init__(*args, **kwargs)
self.loc = jnp.array([locs]).T
self.scale = jnp.array([scales]).T
self.weights = jnp.array([weights]).T
norm = jnp.sum(self.weights)
self.weights = self.weights/norm
self.num_distr = len(locs)
def pdf(self, x):
probs = jax.scipy.stats.norm.pdf(x,loc=self.loc, scale=self.scale)
return jnp.dot(self.weights.T,probs).squeeze()
def logpdf(self, x):
log_probs = jax.scipy.stats.norm.logpdf(x,loc=self.loc, scale=self.scale)
return jax.scipy.special.logsumexp(jnp.log(self.weights) + log_probs, axis=0)
mixture_gaussian_model = MixtureModel_jax([0,1.5],[0.5,0.1],[8,2])
I’m able to generate samples using TansorFlow
import jax
import jax.numpy as jnp
from tensorflow_probability.substrates import jax as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
num_results = int(1e5)
num_burnin_steps = int(1e3)
adaptive_hmc = tfp.mcmc.SimpleStepSizeAdaptation(
tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=mixture_gaussian_model.logpdf, # Here we use the log prob of our known distribtion
num_leapfrog_steps=3,
step_size=1.),
num_adaptation_steps=int(num_burnin_steps * 0.8))
hmc_samples, is_accepted = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=jnp.zeros([2]),
kernel=adaptive_hmc,
trace_fn=lambda _, pkr: pkr.inner_results.is_accepted,
seed=jax.random.PRNGKey(1))
But I cannot manage to transpose to NumpyRo code, is-it possible ?
Thanks
In NumPyro, you can use
kernel = NUTS(potential_fn=lambda x: -mixture_gaussian_model.logpdf(x))
mcmc = MCMC(kernel, num_warmup, num_samples)
mcmc.run(PRNGKey(0), init_params=jnp.zeros(2))
Thanks @fehiepsi although I first get an error and I had to change
my class/logpdf code to get a scalar
def logpdf(self, x):
log_probs = jax.scipy.stats.norm.logpdf(x,loc=self.loc, scale=self.scale)
return jax.scipy.special.logsumexp(jnp.log(self.weights) + log_probs, axis=0)[0]
and I manage to run this code
# Start from this source of randomness. We will split keys for subsequent operations.
rng_key = random.PRNGKey(0)
rng_key, rng_key_ = random.split(rng_key)
# Run NUTS.
kernel = NUTS(potential_fn=lambda x: -mixture_gaussian_model.logpdf(x))
num_samples = 10000
mcmc = MCMC(kernel, num_warmup=1000, num_samples=num_samples, num_chains=2)
mcmc.run(rng_key_, init_params=jnp.zeros(2))
mcmc.print_summary()
samples_1 = mcmc.get_samples()
And get this 1D distrib.
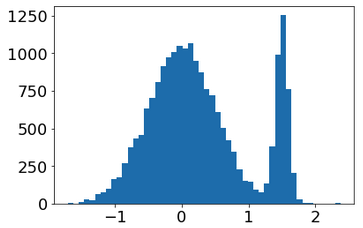
Fine ! do you know how I can modify my code to get a 2D distributions (x,y) with x and y following my 1D distrib. ?
For instance with TF I got
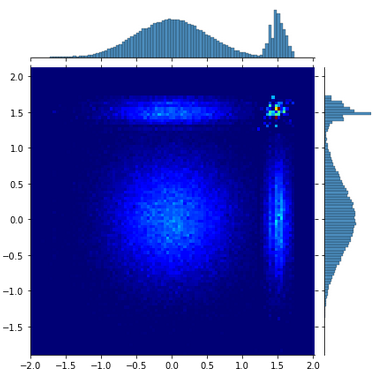
Have you an idea ? Thanks
I think you can use similar code as above. In TFP, you use
target_log_prob_fn=mixture_gaussian_model.logpdf
but in NumPyro, it will be
potential_fn=lambda x, y, z, t: -mixture_gaussian_model.logpdf(x, y, z, t).sum()
i.e. potential_fn is the negative of target_log_prob_fn.
In addition, you need to set init_params in NumPyro to be the same as current_state in TFP.
For multiple chains, you just need to provide a batch of init values. E.g. instead of init_params=jnp.zeros(2), you can provide init_params=jnp.zeros((4, 2)) to specify init values for 4 chains.
there is no a TFP similar mechanism where I do not need to write explicitly all the variables as the number can be 10 or so
Could you be more explicit?
Well, I realized that I had a miss interpretation the 2D plots produced with TF that I have posted. It is the result of the samples of the 1st chain against the 2nd chain if I’m right.
Now, would like to sample a real 2D pdf based on my 1D mixture_gaussian_model with 3 chains for instance (ie. proper initialisation).
Thanks for your kind help.

