Hi, I’m working on a use case which I’m trying to solve using a Pyro bayesian nnet, but for which I cannot get good results. Is anyone interested in taking a look at my approach, and criticise it or help me improving it?
My main concern is that I cannot get my model anywhere near the performance of extremely naive approaches (see below). I read on other posts that if my nr of parameters is much higher than my datapoints, then I wouldn’t be able to get a good performance; but that doesn’t hold in this situation.
The dataset
The dataset is a simplified and preprocessed version of a Kaggle competition dataset, the goal is to predict the arrival delay of flights, from a few features -24 features in total- like “flight distance”, “departure time”, “arrival time”, “origin”, “destination”, etc.
An example of some of the feats:

The training set consists of 4.291.428 flight records (with 24 features each).
The testing set has 922.928 additional samples.
My target distribution looks like the graph below:

The model
I’m modelling the delays with an Exponential distribution, and I’m fitting a bayesian nnet to output its rate based on the features.
Evaluation
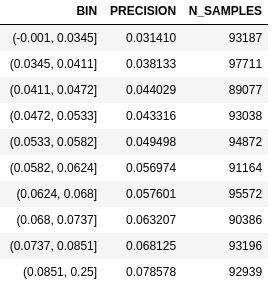
In order to evaluate the output, I use a delay threshold (i.e. 60 min) and I use my model to predict the probability of being delayed more than this threshold. Then I use an uplift curve to compare the models (that is, I get my probability predictions and split them into deciles, for which I compute the precision). See an example in “the baseline” section.
The baseline
As a baseline I’m using the following approaches:
- a groupby mean on categorical features.
- fitting a -non bayesian- nnet with a loss equal to the mean likelihood of the data using different likelihood distributions (e.g. a Gamma).
Next, the results of the groupby baseline:
The code (plus data, plus instructions)