Hi, I am new to Pyro, and I am currently trying to work out examples in this repo: GitHub - CamDavidsonPilon/Probabilistic-Programming-and-Bayesian-Methods-for-Hackers: aka "Bayesian Methods for Hackers": An introduction to Bayesian methods + probabilistic programming with a computation/understanding-first, mathematics-second point of view. All in pure Python ;) using pyro.
As I am working on the example of “An algorithm for human deceit” in Probabilistic-Programming-and-Bayesian-Methods-for-Hackers/Ch2_MorePyMC_PyMC3.ipynb at master · CamDavidsonPilon/Probabilistic-Programming-and-Bayesian-Methods-for-Hackers · GitHub. I have following model setup:
import pyro, torch, pyro.distributions as dist
N = 100
X = 35
def model(X):
p = pyro.sample('freq_cheating', dist.Uniform(0, 1))
with pyro.plate("truth_ans", N):
true_answers = pyro.sample('truths', dist.Bernoulli(p))
first_coin_flips = pyro.sample('first_flips', dist.Bernoulli(0.5))
second_coin_flips = pyro.sample("second_flips", dist.Bernoulli(0.5))
val = pyro.deterministic('val', first_coin_flips*true_answers + (1 - first_coin_flips)*second_coin_flips)
observed_proportion = pyro.deterministic("observed_proportion", torch.sum(val) / N)
observations = pyro.sample("obs", dist.Binomial(total_count=N, probs=observed_proportion), obs=X)
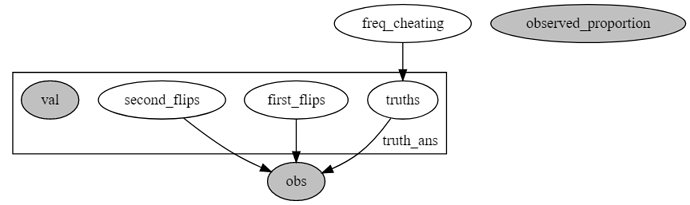
pyro.render_model(model, model_args=(torch.tensor(X), ))
this gives following graph:
which looks weird to me because val and observed_proportion seem to be disconnected from other variables. After I ran following sampling code:
kernel = NUTS(model, jit_compile=True, ignore_jit_warnings=True, max_tree_depth=3)
posterior = MCMC(kernel, num_samples=25000, warmup_steps=15000)
posterior.run(torch.tensor(X));
hmc_samples = {k: v.detach().cpu().numpy() for k, v in posterior.get_samples().items()}
figsize(12.5, 3)
p_trace = hmc_samples["freq_cheating"][15000:]
plt.hist(p_trace, histtype="stepfilled", density=True, alpha=0.85, bins=30,
label="posterior distribution", color="#348ABD")
plt.vlines([.05, .35], [0, 0], [5, 5], alpha=0.3)
plt.xlim(0, 1)
plt.legend();
I found the posterior distribution of freq_cheating is still uniform distribution, meaning the model does not seem to learn anything.
I am wondering if I did something wrong with deterministic, which somehow broke my computation graph, does anyone have any idea?
Thank you!