Understanding how Linear Dynamical Model works in numpyro

numpyro
1

Hi all, I am trying to write a simple Linear Dynamical Model following Bishops definition (Chapter 13.3). In order to understand how to LDM works I first wanted to generate some toy data that I would know the parameters of and then try to predict them.

N_points = 500
A = 0.2
G = 0.5
C = 0.9
S = 1
mu0 = 0
V0 = 1

rng_key_toy_data = random.PRNGKey(33)
rng_key_toy_data, _ = random.split(rng_key_toy_data)

z1 = mu0 + random.normal(rng_key_toy_data) * V0

xs = []

z_prev = z1

for i in range(N_points):
    rng_key_toy_data, _ = random.split(rng_key_toy_data)
    z_t = random.normal(rng_key_toy_data) * G + z_prev * A
    
    rng_key_toy_data, _ = random.split(rng_key_toy_data)
    x_t = random.normal(rng_key_toy_data) * S + z_t * C
    z_prev = z_t
    xs += [x_t]
xs = jnp.array(xs)

So here I have toy data that looks like this:
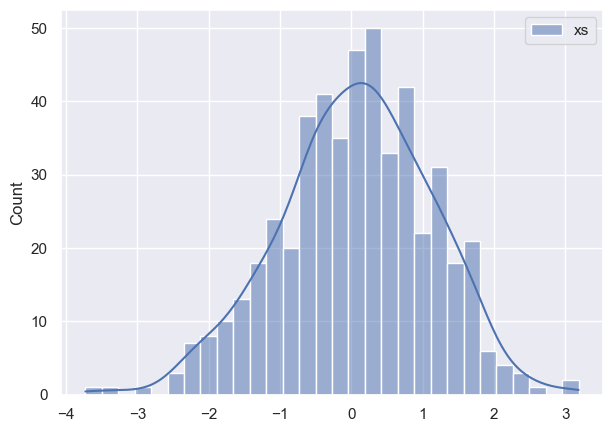
image
So far so good. Now I proceed to creating a model:

def modelToy(obs_data = None):
    L = obs_data.shape[0]
    
    # priors for parameteres
    A = numpyro.sample("A", dist.Normal(1, 1))
    C = numpyro.sample("C", dist.Normal(1, 1))
    
    G = numpyro.sample("G", FoldedStudentT(4, 0.1))
    S = numpyro.sample("S", FoldedStudentT(4, 0.1))
    
    V0 = numpyro.sample("V0", FoldedStudentT(4, 0.1))
    mu0 = numpyro.sample("mu0", dist.Normal(0, 1))
    sigma = numpyro.sample("sigma", FoldedStudentT(4, np.std(obs_data)))
    
    #initial z value
    z1 = numpyro.sample('z1', dist.Normal(mu0, V0))
    
    def chain(z_prev, _):
        z_t = numpyro.sample('z', dist.Normal(A*z_prev, G))
        x_t = numpyro.sample('xt', dist.Normal(C*z_t, S))
        return z_t, x_t
    
    _, x = scan(chain, z1, jnp.arange(L), length=L)
    numpyro.deterministic('x', x)
    
    numpyro.sample("obs", dist.Normal(x, sigma), obs=obs_data)

Here I was trying to follow hmm example. Now I run it:

rng_key = random.PRNGKey(0)
rng_key, rng_key_ = random.split(rng_key)

mcmc = MCMC(NUTS(model=modelToy, adapt_step_size=True, step_size=1e-2), 
            num_samples=2000, 
            num_warmup=10000, 
            num_chains=4)

Now I want to see how posteriors look like and this is where I notice discrepancy:

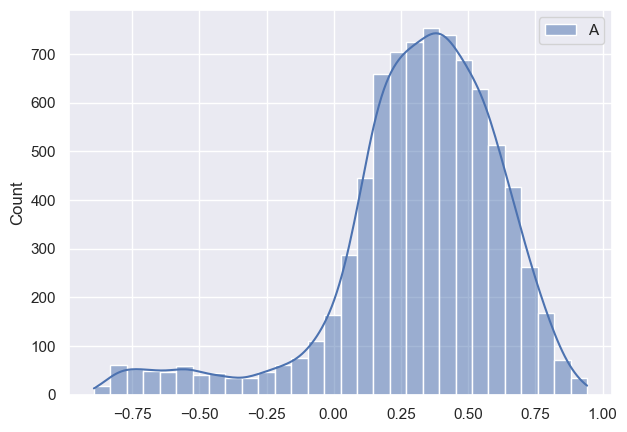
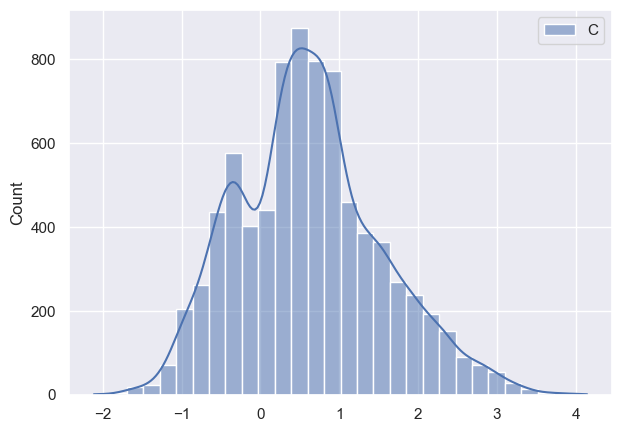
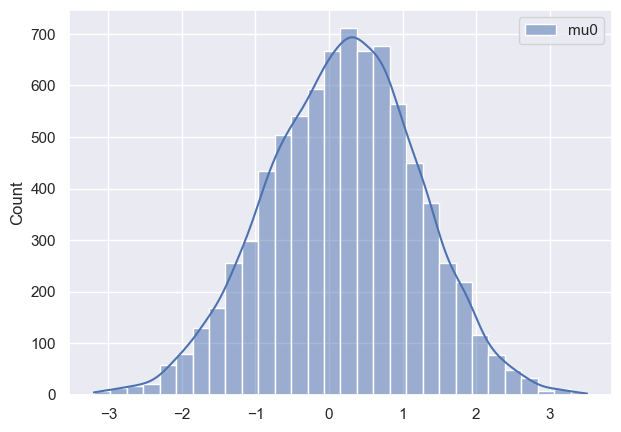
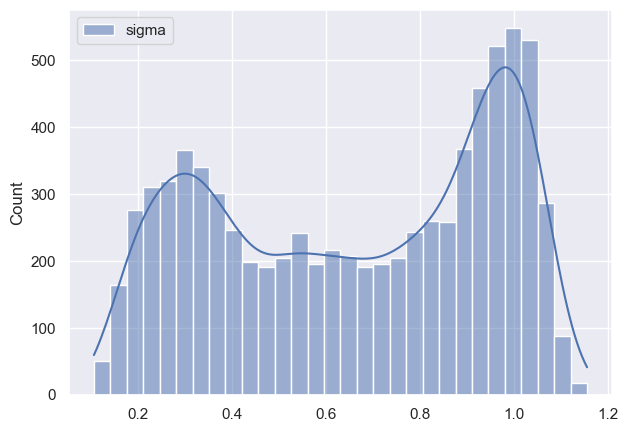
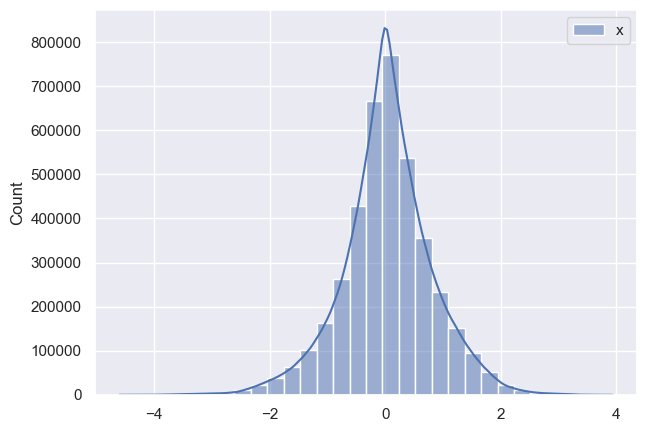
image
image
image
image
image

As it can be seen all parameters have very huge variance and appear bimodal (which I am not sure where it’s coming from, taking into account that I have modeled data). Initially I thought that maybe warm-up phase is not long enough, so I tried increasing it, but nothing changed much. Any suggestions what am I doing wrong?

2

I’m not sure how it is define but it could be that your prior is so strong.

3

Oh sorry my bad

def FoldedStudentT(df, loc=0, scale=1.0):
    return dist.FoldedDistribution(dist.StudentT(df, loc=loc, scale=scale))

I don’t think this is too restrictive prior, I also tried increasing scale here, but the result didn’t differ much.

4

If priors are not informative, you can look at likelihood of the data per each mcmc sample. Then compare with the likelihood of the ground truth parameters.

If priors are informative, you can look at potential energy of the samples and compare them with the true value.

5

Thank, but beside priors being inappropriate is there anything else wrong in my approach?

6

Your model looks reasonable to me.

1 Like
7

Thanks, I will try first for simplicity fixing all parameters except one and try to see how posteriors look like. Building from simplest to the full model.