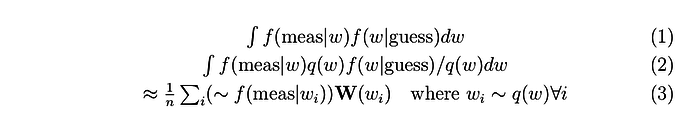I’m new to probabilistic programming. This question pertains to the “Inference in Pyro: From Stochastic Functions to Marginal Distributions” tutorial file.
I’m using pyro version: 0.1.2
In the tutorial
When called with an input guess, marginal first uses posterior to generate a sequence of weighted execution traces given guess, then builds a histogram over return values from the traces, and finally returns a sample drawn from the histogram. Calling marginal with the same arguments more than once will sample from the same histogram.
Just trying to understand what this means mathematically.
My thinking is along the following lines:
Equation (1) represents the marginal we’re trying to compute.
Equation (3) sort of represents what I think is going on.
Steps:
- q(w) is proposal distribution (Q1. Where is q(w) specified in tutorial?)
- Sample
num_sampletimes to getnum_samplesamples of W (importance weight) - Take the max occuring sample (from histogram)
- Sample from f(meas | w) where w is taken from histogram and output as sample from marginal
Am I thinking correctly here?