Trouble sampling from 1D MixtureGeneral

[Pawel]

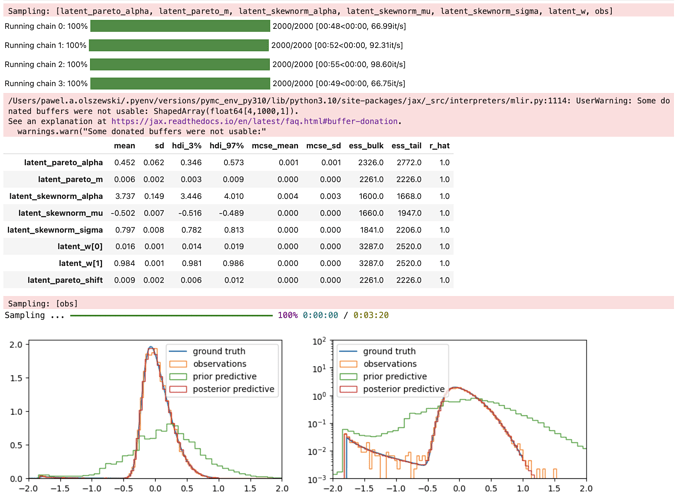
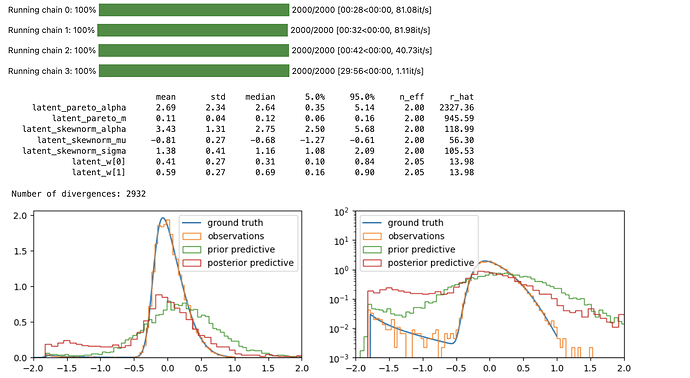
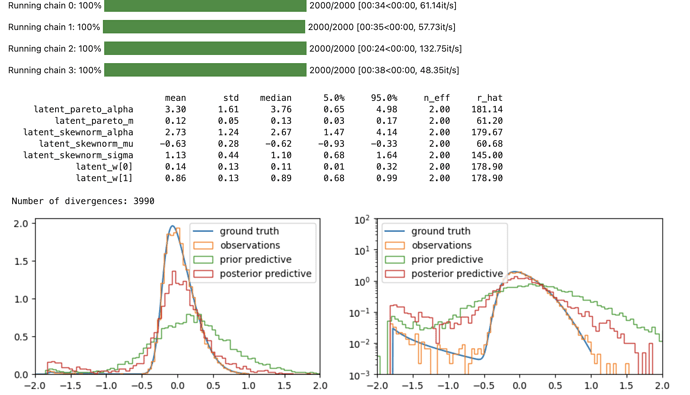
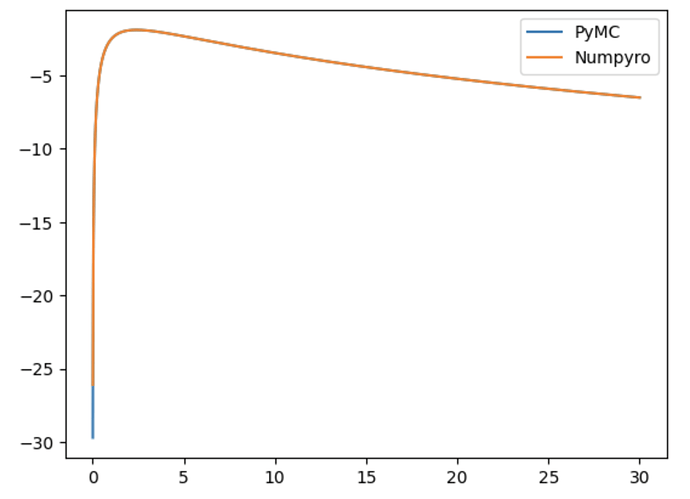
Hi, I’d like to ask for Your help in understading why my numpyro model is sampling very poorly (slow, lots of divergencies, stratospheric r_hat). The reason, why I feel somewhat entitled to being surprised by this poor sampling is that (what I think is) an equivalent model in pymc samples fine (same data, same priors, same model structure, and even using “numpyro” NUTS sampler in pymc). In other words I need help porting a model from pymc to numpyro.

Below I’m pasting my code, including dummy data generations (aligned with the model structure), defining both the pymc and numpyro versions of the model, and the attempts at sampling from both of them.

Few words about the model. It is a somewhat exotic 1D mixture. It’s made out of a) LogSkewNormal which is meant to describe majority of the data, and b) shifted Pareto distribution (ie LogExponential with two-parameter affine transformation on top) which is meant to soak up outliers which are expected to be rare and to lie to the left of the LogSkewNormal.

I’m genuinely invested in trying to fit this model to my real data at work, mostly for inferring parameters of the LogSkewNormal. The dummy data below is similar to one (out of many) of my datasets. And the priors below are fairly genuine: in particular I’m not assuming a priori that the components of the mixture are super well separated, despite the fact the it so happens in the dummy data below.

I’ve also repeated the exercise below but having only one component of the mixture at a time (ie. throwing the other component away from both data generation and the model). In such simple setting both pymc and numpyro models sample equally fine and produce compatible results (fairly correctly inferring the ground truth parameters). This makes me believe that my handmade implementations of LogSkewNormal and ShiftedPareto below are correct (and consistent between pymc and numpyro). That leaves me with the hypothesis that the problem lies somewhere in numpyro’s MixtureGeneral or my usage of it.

I would really appreciate any tips or discussion. Many thanks!

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import bernoulli, pareto, skewnorm

import pymc as pm
import pytensor.tensor as pt

import jax
from jax import lax, random
import jax.numpy as jnp
import numpyro
import numpyro.distributions as dist
import numpyro.handlers as handl
from numpyro.infer import MCMC, NUTS, SVI, Predictive, Trace_ELBO, autoguide
import optax

rng = np.random.default_rng(0)
numpyro.util.set_host_device_count(4)
rng_key = random.PRNGKey(0)

# GROUND TRUTH

w = 0.015
pareto_alpha = 0.5
pareto_m = 0.007
pareto_shift = 0.008
skewnorm_mu = -0.5
skewnorm_sigma = 0.8
skewnorm_alpha = 3.8

## GENERATE DATA

N = 10_000
_w = bernoulli(p=w).rvs(size=N, random_state=rng)
pareto_rvs = pareto(b=pareto_alpha, loc=pareto_shift, scale=pareto_m).rvs(size=N, random_state=rng)
logskewnorm_rvs = np.exp(skewnorm(a=skewnorm_alpha, loc=skewnorm_mu, scale=skewnorm_sigma).rvs(size=N, random_state=rng))
rvs = _w * pareto_rvs + (1 - _w) * logskewnorm_rvs

# PYMC MODEL

def _shiftedpareto_dist(alpha, m, shift, size):
    return pm.Pareto.dist(alpha=alpha, m=m, size=size) + shift


def _logskewnorm_dist(mu, sigma, alpha, size):
    return pt.exp(pm.SkewNormal.dist(mu=mu, sigma=sigma, alpha=alpha, size=size))


with pm.Model() as pymc_model:

    latent_pareto_alpha = pm.TruncatedNormal("latent_pareto_alpha", mu=2, sigma=2, lower=1e-2, upper=6.0)
    latent_pareto_m = pm.TruncatedNormal("latent_pareto_m", mu=0.0, sigma=0.1, lower=1e-3, upper=0.2)
    latent_pareto_shift = pm.Deterministic("latent_pareto_shift", rvs.min() - latent_pareto_m)

    leftoutlier_dist = pm.CustomDist.dist(
        latent_pareto_alpha, latent_pareto_m, latent_pareto_shift,
        dist=_shiftedpareto_dist,
        class_name="ShiftedPareto")
    
    latent_skewnorm_alpha = pm.TruncatedNormal("latent_skewnorm_alpha", mu=3, sigma=2, lower=-1, upper=7)
    latent_skewnorm_mu = mu = pm.TruncatedNormal("latent_skewnorm_mu", mu=0.0, sigma=1, lower=-3, upper=3)
    latent_skewnorm_sigma = pm.HalfNormal("latent_skewnorm_sigma", 1)

    main_dist = pm.CustomDist.dist(
        latent_skewnorm_mu, latent_skewnorm_sigma, latent_skewnorm_alpha,
        dist=_logskewnorm_dist,
        class_name="LogSkewNormal")

    latent_w = pm.Dirichlet('latent_w', a=np.array([1, 30]))

    obs = pm.Mixture(
        'obs',
        w=latent_w,
        comp_dists=[leftoutlier_dist, main_dist],
        observed=rvs)

# PYMC PRIOR PREDICTIVE

with pymc_model:
    pymc_prior_pred = pm.sample_prior_predictive(500)

pymc_prior_obs = pymc_prior_pred.prior_predictive["obs"].values.reshape(-1)

# PYMC MCMC

with pymc_model:
    pymc_trace = pm.sample(nuts_sampler="numpyro")

display(pm.summary(pymc_trace))

# PYMC POSTERIOR PREDICTIVE

with pymc_model:
    pymc_post_pred = pm.sample_posterior_predictive(pymc_trace)

pymc_post_obs = pymc_post_pred.posterior_predictive["obs"].values.reshape(-1)

# PLOT GROUND TRUTH, OBSERVATIONS, PYMC PRIOR- AND POSTERIOR PREDICTIVES,
# use log-scale(s)

x = np.linspace(0, 10, 3_000)[1:]
y = (
    w * pareto(b=pareto_alpha, loc=pareto_shift, scale=pareto_m).pdf(x)
    + (1 - w) * skewnorm(a=skewnorm_alpha, loc=skewnorm_mu, scale=skewnorm_sigma).pdf(np.log(x))/x)

rvs_p99 = rvs[rvs < np.percentile(rvs, 99)]
pymc_prior_obs_p999 = pymc_prior_obs[(pymc_prior_obs < np.percentile(pymc_prior_obs, 99.9))]
pymc_post_obs_p9999 = pymc_post_obs[
    (pymc_post_obs < np.percentile(pymc_post_obs, 99.99))]

fig, axs = plt.subplots(1, 2, figsize=(12, 3))

for ax in axs:
    ax.plot(np.log10(x), y * x * np.log(10), label="ground truth");
    ax.hist(np.log10(rvs), density=True, bins=100, histtype="step", label="observations");
    ax.hist(np.log10(pymc_prior_obs_p999), density=True, bins=100, histtype="step", label="prior predictive");
    ax.hist(np.log10(pymc_post_obs_p9999), density=True, bins=100, histtype="step", label="posterior predictive");
    ax.legend();
    ax.set_xlim(-2, 2);
    
axs[1].set_yscale("log");
axs[1].set_ylim(1e-3, 1e2);

# NUMPYRO MODEL

class ShiftedPareto(dist.TransformedDistribution):
    arg_constraints = {"scale": dist.constraints.positive, "alpha": dist.constraints.positive}
    reparametrized_params = ["scale", "alpha"]

    def __init__(self, loc, scale, alpha, *, validate_args=None):
        self.loc, self.scale, self.alpha = dist.util.promote_shapes(loc, scale, alpha)
        batch_shape = lax.broadcast_shapes(jnp.shape(loc), jnp.shape(scale), jnp.shape(alpha))
        loc, scale, alpha = (
            jnp.broadcast_to(loc, batch_shape),
            jnp.broadcast_to(scale, batch_shape),
            jnp.broadcast_to(alpha, batch_shape),
        )
        base_dist = dist.Exponential(alpha)
        transforms = [
            dist.transforms.ExpTransform(),
            dist.transforms.AffineTransform(loc=loc, scale=scale)
        ]
        super(ShiftedPareto, self).__init__(base_dist, transforms, validate_args=validate_args)

    @dist.constraints.dependent_property(is_discrete=False, event_dim=0)
    def support(self):
        return dist.constraints.greater_than(self.loc + self.scale)


class SkewNormal(dist.Distribution):
    arg_constraints = {"mu": dist.constraints.real, "sigma": dist.constraints.positive, "alpha": dist.constraints.real}
    support = dist.constraints.real
    reparametrized_params = ["mu", "sigma", "alpha"]

    def __init__(self, mu=0.0, sigma=1.0, alpha=0.0, *, validate_args=None):
        self.mu, self.sigma, self.alpha = dist.util.promote_shapes(mu, sigma, alpha)
        self.tau = 1 / self.sigma ** 2
        batch_shape = lax.broadcast_shapes(jnp.shape(mu), jnp.shape(sigma), jnp.shape(alpha))
        super(SkewNormal, self).__init__(
            batch_shape=batch_shape, validate_args=validate_args
        )

    @dist.util.validate_sample
    def log_prob(self, value):
        # https://github.com/pymc-devs/pymc/blob/36cca5b623dda4e75ac677c9d8ad6a321a2e72c2/pymc/distributions/continuous.py#L3149
        
        return (
            jnp.log1p(jax.scipy.special.erf((value - self.mu) / self.sigma * self.alpha / jnp.sqrt(2)))
            + (-self.tau * (value - self.mu) ** 2 + jnp.log(self.tau / jnp.pi / 2.0)) / 2.0
        )

    def sample(self, key, sample_shape=()):
        # https://github.com/scipy/scipy/blob/92d2a8592782ee19a1161d0bf3fc2241ba78bb63/scipy/stats/_continuous_distns.py#L9422
        
        assert numpyro.util.is_prng_key(key)
        key_1, key_2 = random.split(key)
        shape = sample_shape + self.batch_shape + self.event_shape
        
        u0 = random.normal(key_1, shape=shape)
        v = random.normal(key_2, shape=shape)
        d = self.alpha/jnp.sqrt(1 + self.alpha**2)
        u1 = d*u0 + v * jnp.sqrt(1 - d**2)
        _rvs = jnp.where(u0 >= 0, u1, -u1)
        
        rvs = _rvs * self.sigma + self.mu
        return rvs


class LogSkewNormal(dist.TransformedDistribution):
    arg_constraints = {"mu": dist.constraints.real, "sigma": dist.constraints.positive, "alpha": dist.constraints.real}
    support = dist.constraints.positive
    reparametrized_params = ["mu", "sigma", "alpha"]

    def __init__(self, mu=0.0, sigma=1.0, alpha=0.0, *, validate_args=None):
        base_dist = SkewNormal(mu, sigma, alpha)
        self.mu, self.sigma, self.alpha = base_dist.mu, base_dist.sigma, base_dist.alpha
        super(LogSkewNormal, self).__init__(
            base_dist, dist.transforms.ExpTransform(), validate_args=validate_args
        )


def numpyro_model(n_obs):

    latent_pareto_alpha = numpyro.sample("latent_pareto_alpha", dist.TruncatedNormal(loc=2, scale=2, low=1e-2, high=6))
    latent_pareto_m = numpyro.sample("latent_pareto_m", dist.TruncatedNormal(loc=0, scale=0.1, low=1e-3, high=0.2))
    latent_pareto_shift = numpyro.deterministic("latent_pareto_shift", rvs.min() - latent_pareto_m)

    leftoutlier_dist = ShiftedPareto(
        loc=latent_pareto_shift, scale=latent_pareto_m, alpha=latent_pareto_alpha)

    latent_skewnorm_alpha = numpyro.sample("latent_skewnorm_alpha", dist.TruncatedNormal(loc=3, scale=2, low=-1, high=7))
    latent_skewnorm_mu = numpyro.sample("latent_skewnorm_mu", dist.TruncatedNormal(loc=0, scale=1, low=-3, high=3))
    latent_skewnorm_sigma = numpyro.sample("latent_skewnorm_sigma", dist.HalfNormal(scale=1))

    main_dist = LogSkewNormal(
        mu=latent_skewnorm_mu, sigma=latent_skewnorm_sigma, alpha=latent_skewnorm_alpha)

    latent_w = numpyro.sample("latent_w", dist.Dirichlet(concentration=jnp.array([1.0, 30.0])))

    with numpyro.plate("obs_plate", n_obs):
        obs = numpyro.sample(
            "obs",
            dist.MixtureGeneral(
                mixing_distribution=dist.Categorical(probs=latent_w),
                component_distributions=[leftoutlier_dist, main_dist],
                support=dist.constraints.positive))

# NUMPYRO PRIOR PREDICTIVE

rng_key, rng_key_ = random.split(rng_key)
numpyro_prior_pred = Predictive(numpyro_model, num_samples=10_000)(rng_key_, n_obs=1)
numpyro_prior_obs = numpyro_prior_pred["obs"].reshape(-1)

# NUMPYRO MCMC

numpyro_mcmc = MCMC(
    sampler=NUTS(handl.condition(numpyro_model, {"obs": rvs})),
    num_warmup=1_000,
    num_samples=1_000,
    num_chains=4,
)
rng_key, rng_key_ = random.split(rng_key)
numpyro_mcmc.run(rng_key_, n_obs=len(rvs))
numpyro_mcmc.print_summary()
numpyro_mcmc_samples = numpyro_mcmc.get_samples(group_by_chain=True)

# NUMPYRO POSTERIOR PREDICTIVE

rng_key, rng_key_ = random.split(rng_key)
numpyro_post_pred = Predictive(numpyro_model, posterior_samples=numpyro_mcmc_samples)(rng_key_, n_obs=1)
numpyro_post_obs = numpyro_post_pred["obs"].reshape(-1)

# PLOT GROUND TRUTH, OBSERVATIONS, NUMPYRO PRIOR- AND POSTERIOR PREDICTIVES,
# use log-scale(s)

rvs_p99 = rvs[rvs < np.percentile(rvs, 99)]
numpyro_prior_obs_p999 = numpyro_prior_obs[(numpyro_prior_obs < np.percentile(numpyro_prior_obs, 99.9))]
numpyro_post_obs_p9999 = numpyro_post_obs[
    (numpyro_post_obs < np.percentile(numpyro_post_obs, 99.99))]

fig, axs = plt.subplots(1, 2, figsize=(12, 3))

for ax in axs:
    ax.plot(np.log10(x), y * x * np.log(10), label="ground truth");
    ax.hist(np.log10(rvs), density=True, bins=100, histtype="step", label="observations");
    ax.hist(np.log10(numpyro_prior_obs_p999), density=True, bins=100, histtype="step", label="prior predictive");
    ax.hist(np.log10(numpyro_post_obs_p9999), density=True, bins=100, histtype="step", label="posterior predictive");
    ax.legend();
    ax.set_xlim(-2, 2);
    
axs[1].set_yscale("log");
axs[1].set_ylim(1e-3, 1e2);

[fehiepsi]

I think you can check for agreements between two implementation by:

• check log_prob of each random variables in your model
• check support of each random variables in your model

[Pawel]

Thanks for the response!
Any pointers how to go about checking these two in numpyro? (or in pymc for that matter?)
I’m rather new to numpyro Also I’m not sure if I’m following conceptually

1. By checking log_prob of a random_variable You mean storing an additional deterministic quantity in my MCMC chain along these lines:

dist_instance = my_dist(...)
my_latent_var = numpyro.sample("my_latent_var", dist_instance)
numpyro.deterministic("my_latent_var_logprob", dist_instance.log_prob(my_latent_var))

What would I be looking for? If and how the distributions of such logprobs differs between pymc and numpyro?

2. By checking support for a random variable do You mean inspecting min/max values achieved by this variable in the MCMC traces?

[fehiepsi]

To get log_prob and support of a distribution d, you can do d.log_prob(value) and d.support. It is better to not build a numpyro model to check those information. Make it simple first, for example,

d = dist.Normal(0, 1)
print(d.log_prob(10))
print(d.support)

I’m not familiar with PyMC but I think you can also do similar checks there.

[martinjankowiak]

i have no idea what’s going on but some things to look into might be your custom log_prob for SkewNormal and the usage of dependent constraints

[Pawel]

some things to look into might be your […] usage of dependent constraints

I got to admit that I’ve written the above ShiftedPareto and LogSkewNormal for numpyro by mimicking numpyro’s source code (eg. for Pareto and LogNormal dists), often without understanding. Could You please tell what You mean by dependent contraints and where am I using them?

[Pawel]

hmm…, having just thrown away this part

    @dist.constraints.dependent_property(is_discrete=False, event_dim=0)
    def support(self):
        return dist.constraints.greater_than(self.loc + self.scale)

from the definition of ShiftedPareto, and running the numpyro code again, I’m getting a somewhat different behaviour: the sampling goes much faster with more divergencies, but the resulting posterior seems to be pulled slightly more into the right direction…

[Pawel]

I’m thinking the inclusion/exclusion of the left boundary of Pareto’s support might be an issue

• Textbook-wise pdf of Pareto (of scale=1) seems to be usually defined on [1, inf), jax.random.pareto — JAX documentation, Pareto distribution - Wikipedia, and PyMC follows that convention.
• But the implementation in numpyro seems to exclude the left boundary, since the distribution is literally an ExpTransform of dist.Exponential (numpyro.distributions.continuous — NumPyro documentation) The latter’s support is strictly positive, so Pareto’s support would be strictly greater than 1. Which is also consistent with numpyro’s explicitly defined dist.Pareto.support. On the other hand dist.Pareto.log_prob returns finite values for all positive arguments even outside of its support:

dist_ = dist.Pareto(1, 1)
dist_.support, dist_.log_prob(0.5)

[fehiepsi]

You can enable the support validation via numpyro.enable_validation() Runtime Utilities — NumPyro documentation

[Pawel]

I think you can check for agreements between two implementation by:

• check log_prob of each random variables in your model
• check support of each random variables in your model

I’ve checked that the two above implementations, in PyMC and Numpyro, use the same log_probs, for both the LogSkewNormal and ShiftedPareto, in the sense that I’ve explicitly compared their values obtained for a couple of top-of-my-head choices of their parameters, for a - hopefully sensibly wide - range of x values. I’m pasting an example of such comparison below. This makes me believe that the log_probs are indeed matching.

def _logskewnorm_dist(mu, sigma, alpha, size):
    return pt.exp(pm.SkewNormal.dist(mu=mu, sigma=sigma, alpha=alpha, size=size))
    
dist_skewnorm_pymc = pm.CustomDist.dist(
        1, 1, 1,  # mu, sigma, alpha
        dist=_logskewnorm_dist,
        class_name="LogSkewNormal")

dist_skewnorm_numpyro = LogSkewNormal(mu=1, sigma=1, alpha=1)

x = np.linspace(1e-2, 30, 10_000)
_logp_pymc = pm.logp(dist_skewnorm_pymc, x).eval()
_logp_numpyro = dist_skewnorm_numpyro.log_prob(x)

plt.plot(x, _logp_pymc, label="PyMC")
plt.plot(x, _logp_numpyro, label="Numpyro")
plt.legend();

I haven’t found an attribute or method in PyMC distributions that would explicitly encode the support, but the PyMC log_probs are behaving as expected with respect to returning infinities (or nans) outside of their support: in particular the log-transformed SkewNormal returns finite log_probs only for strictly positive values, and the ShiftedPareto returns finite log_probs only for values gte than loc+scale (both can also blow up from within their support when they’re calculated close enough to the support’s boundary, where “close enough” depends on the distribution’s parameters).

[fehiepsi]

You can get the desired out-of-support values by setting validate_args=True. From your comment, it seems that the component log probs agree on the domain. Have you check the mixture log prob? Its domain is positive as in your definition.

[Pawel]

Have you check the mixture log prob?

Right, I have checked it only now, but it seems ok as well:
In Numpyro the LogSkewNorm’s logprob is blowing up further away from zero than in PyMC but that’s, I’m guessing, due to using single rather than double precision. Other than that, the logprobs are the same. Here’s an example:

w = 0.015
pareto_alpha = 0.5
pareto_m = 0.01
pareto_shift = 0.02
skewnorm_mu = -0.5
skewnorm_sigma = 0.8
skewnorm_alpha = 1

# Numpyro dists
dist_pareto_numpyro = ShiftedPareto(loc=pareto_shift, scale=pareto_m, alpha=pareto_alpha)
dist_skewnorm_numpyro = LogSkewNormal(mu=skewnorm_mu, sigma=skewnorm_sigma, alpha=skewnorm_alpha)
dist_mixture_numpyro = dist.MixtureGeneral(
    mixing_distribution=dist.Categorical(probs=jnp.array([w, 1 - w])),
    component_distributions=[dist_pareto_numpyro, dist_skewnorm_numpyro],
    support=dist.constraints.positive)

# PyMC dists
def _shiftedpareto_dist(alpha, m, shift, size):
    return pm.Pareto.dist(alpha=alpha, m=m, size=size) + shift
    
dist_pareto_pymc = pm.CustomDist.dist(
    pareto_alpha, pareto_m, pareto_shift,  # alpha, m, shift
    dist=_shiftedpareto_dist,
    class_name="ShiftedPareto")

def _logskewnorm_dist(mu, sigma, alpha, size):
    return pt.exp(pm.SkewNormal.dist(mu=mu, sigma=sigma, alpha=alpha, size=size))
    
dist_skewnorm_pymc = pm.CustomDist.dist(
    skewnorm_mu, skewnorm_sigma, skewnorm_alpha,  # mu, sigma, alpha
    dist=_logskewnorm_dist,
    class_name="LogSkewNormal")

dist_mixture_pymc = pm.Mixture.dist(
    w=np.array([w, 1 - w]),
    comp_dists=[dist_pareto_pymc, dist_skewnorm_pymc])

# plot
x = np.linspace(0, 3, 100_000)[1:]
y_numpyro = dist_mixture_numpyro.log_prob(x)
y_pymc = pm.logp(dist_mixture_pymc, x).eval()

plt.plot(x, y_pymc, linewidth=6, label="pymc logprob")
plt.plot(x, y_numpyro, linewidth=3, label="numpyro logprob")
plt.axvline(pareto_shift + pareto_m, linestyle=":", c="k", label="Pareto support boundary")
plt.xscale("log")
plt.legend();

[martinjankowiak]

are you using double precision for inference? numpyro.enable_x64()

[Pawel]

are you using double precision for inference? numpyro.enable_x64()

Thanks, I wasn’t aware of this util!
I was using single precision in Numpyro in this story so far. I’ve just rerun everything with numpyro.util.enable_x64() prepended to my code above and I’ve got the exact same summary from numpyro (and posterior plot) as pasted above.

I was hoping the increased precision would be the solution that I’m looking for, but it seems not. The fact that I’m getting the exact same values in my summary table with and without x64 is surprising to me, since I would expect to see some small numerical discrepancy…

But the last plot of the mixture’s log_prob is now matching exactly between numpyro and PyMC

[fehiepsi]

It took me a couple of hours to debug this. This is a bit subtle. The main issue is “log1p(erf(x))” is not numerical stable. I’m not sure how pymc deals with this (maybe they truncate / clip things or their numerical system is more numerical stable than jax). My solution is to replace log1p(erf(x)) by

def log1p_erf(x):
    neg_x = jnp.where(x > 0, 0, x)
    pos_x = jnp.where(x > 0, x, 0)
    return jnp.where(x < 0, jnp.log(jax.scipy.special.erfc(-neg_x)), jnp.log1p(jax.scipy.special.erf(pos_x)))

How did I debug this issue? (posting here in case someone is interested in)

• Based on the last comment, it seems that the likelihood is computed correctly but I wanted to double check. I computed the log likelihood inside the model and add the statement deterministic("ll", loglik). Then I print their summary via mcmc.print_summary(exclude_deterministic=False). Loglik of numpyro samples is much smaller than of the ground truth value, which is expected → the issue is likely not due to the likelihood computation
• Then I froze most of the parameters (replace the numpyro.sample(...) variables by their ground truth value), except for latent_w and latent_skewnorm_alpha. The issue still happens. → numerical happens somewhere.
• Using jax.debug_nans (jax.debug_nans — JAX documentation), I found that it belongs to the line computing log1p(erf(x)). I asked chatgpt for a better implementation - it suggested to deal with neg x and pos x separately. → applying the solution leads to the desired result.

[OlaRonning]

Thanks for sharing the debug story. I must admit, I initially found the solution somewhat unusual, so I decided to investigate further. By replacing log1p(erf(x)) with log(erfc(-x)), you gain the advantage of long integration for negative numbers while maintaining minimal error for positive numbers because the log grows a lot slower for log(2>x>1) than log(0<x<1).

umpyro.enable_x64()

x = jnp.linspace(-10, 100, 10_000)
l1p_erf = jnp.log1p(erf(x))
l_erfc = jnp.log(erfc(-x))

print(f"{jnp.linalg.norm(l1p_erf[x>=0] - l_erfc[x>=0])}")  # ~1e-15

[fehiepsi]

Yeah it might be enough to use log(erfc). Would be useful to also look at grad because NaN also happens at grad IIRC.

I havent tested but maybe it is more stable to use log_ndtr jax.scipy.special.log_ndtr — JAX documentation directly.

[OlaRonning]

Well, it turns out that the gradients are also well-behaved for log(erfc), but not for logp1(erf).