Toy regression example infers identical variance for all RVs

numpyro
1

Hi all,

I am working on a toy example that learns the influence of binary configuration options on some non-functional property with the influences being my random variables. Although I implemented my artificial toy target function such that the influence of option A varies largely, NUTS infers all influences with the same variance.

This is my code:

def ask_oracle(config):
    base = 20
    a, b, c = config
    influence_a = scipy.stats.norm(5, 3).rvs(1)[0]
    influence_b = 0.5
    influence_c = 2
    nfp = influence_a * a + influence_b * b + influence_c * c + base
    return nfp

Here, we define that influence_a should be normal-distributed with mean 5 and stddev 3.

This is my model:

def model(a, b, c, obs=None):
    mean = 0
    var = 15
    influence_a = numpyro.sample("influence_a", npdist.Normal(mean, var))
    influence_b = numpyro.sample("influence_b", npdist.Normal(mean, var))
    influence_c = numpyro.sample("influence_c", npdist.Normal(mean, var))
    base = numpyro.sample("base", npdist.HalfNormal(30))
    result = base + a * influence_a + b * influence_b + c * influence_c
    error_var = numpyro.sample("error", npdist.HalfNormal(1.0))
    with numpyro.plate("data", len(a)):
        obs = numpyro.sample("nfp", npdist.Normal(result, error_var), obs=obs)
    return obs

And this is my experiment:

def main():
    configs = list(itertools.product([True, False], repeat=3))
    configs = configs * 20 # simulating repeated measurements
    python_random.shuffle(configs)
    nfp = jnp.atleast_1d(list(map(ask_oracle, configs)))
    X = jnp.atleast_2d(configs)
    X = MinMaxScaler().fit_transform(X)
    nuts_kernel = npNUTS(model)
    n_chains = 3
    mcmc = npMCMC(nuts_kernel, num_samples=2000,
                  num_warmup=5000, progress_bar=False, num_chains=n_chains)
    rng_key = random.PRNGKey(0)
    mcmc.run(rng_key, X[:, 0], X[:, 1], X[:, 2], obs=nfp)

    mcmc.print_summary()
    az_data = az.from_numpyro(mcmc, num_chains=n_chains)
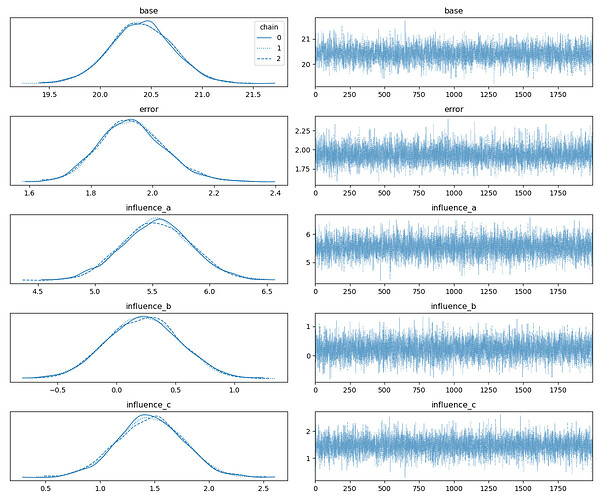
    az.plot_trace(az_data, legend=True,)

This is the output:

                   mean       std    median      5.0%     95.0%     n_eff     r_hat
         base     20.41      0.31     20.41     19.93     20.93   3693.94      1.00
        error      1.93      0.11      1.93      1.75      2.10   5030.02      1.00
  influence_a      5.54      0.30      5.54      5.02      6.02   4867.74      1.00
  influence_b      0.23      0.31      0.23     -0.26      0.76   4564.49      1.00
  influence_c      1.46      0.30      1.46      0.98      1.97   4685.77      1.00

toy-abc-example-trace
toy-abc-example-trace1200×1000 279 KB

I assumed that MCMC would assign more uncertainty to option A’s influence instead of the other RVs in order to approach the posterior more closely.
What can I do to detect this varying uncertainty? Is this generally possible?

2

not sure about your broader question but the second argument to a numpyro Normal distribution is a square root variance (scale) and not a variance

3

thanks for the heads-up! All variances should be standard deviations in my post, consequently. The standard deviation for influence_a should still be larger than the others. Does anyone else have an idea what I am doing wrong?