Hi, I’m using pyro 1.9.1 - I have ultrasonic vectors 3250 long normalized on [-1,1]
I am running the following model:
def plot_ascan():
data = train_loader.dataset.__getitem__(425000)
fig, ax = plt.subplots(2, 1, squeeze=False)
ax[0, 0].plot(vae.reconstruct_img(data[0].cuda()).detach().cpu().numpy().T)
ax[0, 0].plot(data[0].detach().cpu().numpy())
ax[1, 0].plot(train_elbo)
class Decoder(nn.Module):
def __init__(self, z_dim, hidden_dim, data_dim):
super().__init__()
self.fc1 = nn.Sequential(
nn.Linear(z_dim, hidden_dim),
nn.ELU(),
nn.Linear(hidden_dim, hidden_dim),
nn.ELU(),
nn.Linear(hidden_dim, data_dim),
)
def forward(self, z):
return self.fc1(z)
class Encoder(nn.Module):
def __init__(self, z_dim, hidden_dim, data_dim):
super().__init__()
self.fc1 = nn.Sequential(
nn.Linear(data_dim, hidden_dim),
nn.ELU(),
nn.Linear(hidden_dim, hidden_dim),
nn.ELU(),
)
# distribution parameters
self.fc_mu = nn.Linear(hidden_dim, z_dim)
self.fc_scale = nn.Linear(hidden_dim, z_dim)
self.z_dim = z_dim
self.hidden_dim = hidden_dim
self.data_dim = data_dim
def forward(self, x):
hidden = self.fc1(x)
mu = self.fc_mu(hidden)
scale = torch.exp(self.fc_scale(hidden))
return mu, scale
class VAE(nn.Module):
def __init__(self, z_dim, hidden_dim, data_dim, use_cuda):
super().__init__()
# create the encoder and decoder networks
self.encoder = Encoder(z_dim, hidden_dim, data_dim)
self.decoder = Decoder(z_dim, hidden_dim, data_dim)
self.z_dim = z_dim
self.hidden_dim = hidden_dim
self.data_dim = data_dim
self.cuda()
self.use_cuda = use_cuda
# define the model p(x|z)p(z)
def model(self, x):
pyro.module("decoder", self.decoder)
with pyro.plate("data", x.shape[0]):
mu = x.new_zeros(torch.Size((x.shape[0], self.z_dim)))
scale = x.new_ones(torch.Size((x.shape[0], self.z_dim)))
z = pyro.sample("latent", dist.Normal(mu, scale).to_event(1))
loc_img = self.decoder(z)
# pyro.sample("obs", dist.Bernoulli(loc_img).to_event(1), obs=x.reshape(-1, self.data_dim))
pyro.deterministic("obs", loc_img)
# define the guide (i.e. variational distribution) q(z|x)
def guide(self, x):
pyro.module("encoder", self.encoder)
with pyro.plate("data", x.shape[0]):
mu, scale = self.encoder(x)
pyro.sample("latent", dist.Normal(mu, scale).to_event(1))
# define a helper function for reconstructing images
def reconstruct_img(self, x):
mu, scale = self.encoder(x)
z = dist.Normal(mu, scale).sample()
loc_img = self.decoder(z)
return loc_img
def train(svi, train_loader):
epoch_loss = 0.0
for x, _ in train_loader:
x = x.cuda()
epoch_loss += svi.step(x)
# return epoch loss
normalizer_train = len(train_loader.dataset)
total_epoch_loss_train = epoch_loss / normalizer_train
return total_epoch_loss_train
train_loader, test_loader = setup_data_loaders(lo, hi, 512, True)
lr = 1.0e-4
epochs = 100
TEST_FREQUENCY = 5
z = 512
hidden_dim = 2048
cuda = True
pyro.clear_param_store()
vae = VAE(z, hidden_dim, data_dim, cuda)
adam_args = {"lr": lr}
optimizer = Adam(adam_args)
loss_function = Trace_ELBO()
loss_function = TraceMeanField_ELBO()
svi = SVI(vae.model, vae.guide, optimizer, loss=loss_function)
train_elbo = []
test_elbo = []
for epoch in range(epochs):
total_epoch_loss_train = train(svi, train_loader)
train_elbo.append(-total_epoch_loss_train)
print("[epoch %03d] average training loss: %.8f" % (epoch, total_epoch_loss_train))
Which is taken directly from the VAE tutorial, with some slight modifications, in particular my use of pyro.deterministic(“obs”, loc_img) in the model.
The model is based on a working pytorch implementation.
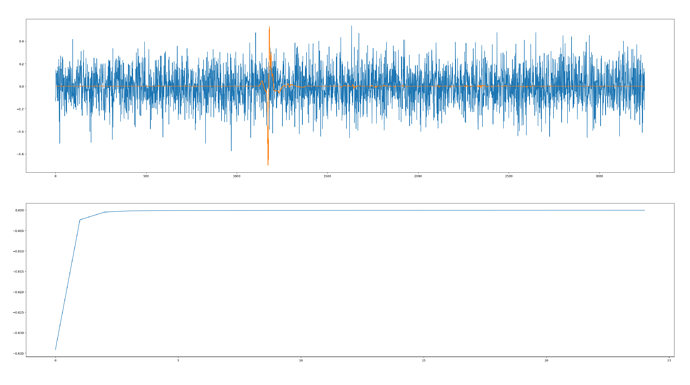
My problem here is shown in the image below - taken after almost 25 epochs of training.
The orange is my training data, the blue is the decoded latents (as per the reconstruct_img() function) and the second plot is my loss. So the loss curve looks great, but my latents don’t appear to be informative.
Any ideas what I am doing wrong here?
I