Hello everyone! 
As promised, i give an update and summary on our findings regarding the SBM implementation in Pyro.
In general, we haven’t been able to obtain a fully-functioning SBM model using solely the tools and methods provided by Pyro itself. There are many reasons as to why and these themselves are quite dependent on the respective approach we tried using. Note that we decided for an SVI inference solution.
In our first model implementations as for instance, we focused on the GMM example as it is very similar to the SBM in its nature. However, here we encountered issues with the “learning” process. To make it short, membership inference worked well - at least for a very simple toy example with two communities - if and only if the Stochastic Block Matrix was initialized/learned properly in the first place. This resulted in us trying various approaches to accurately estimate the block matrix parameters using Pyro. In the end though, this has not worked at all meaning that we weren’t able to obtain a “closed-form” inference solution. We also tried using an auto_guide as suggested in the GMM documentation with the hope for a better parameter initialization, unfortunately without much success. The problem simply persisted in a more or less biased block matrix initialization we couldn’t get rid off.
Some other things we also considered were:
- Switch to TraceGraph_ELBO to eliminate high variance we encountered during inference
- Apply separate model/guide pairs for block matrix parameter learning and membership inference
- Increase the number of particles (num_particles) in the loss settings for a more granular inference (note that this takes significantly more time in computing the solution)
- MAP inference approach motivated by edward1 (TensorFlowProbability)
- Variations in Multinomial/Categorical realizations of the model
- Enumeration in very early models (mostly did not work because of dimensionality issues)
To summarize, inference results were quite frustrating. Either, we did not infer correctly or we ended up with a perfectly random solution, that is a membership probability of ~50% for either group. Also note that for debugging and testing reasons, we switched from the already simple karate club data set to an even simpler toy data set where two groups are connected to each other by only a single edge and the respective nodes in themselves are fully connected with each other. With that in mind, we were even more frustrated with the results as we could not have fabricated a more basic example as this one. Also, computation/inference time was exhaustingly long with some of above variations - such as the block matrix parameter learning + subsequent inference with increased num_particles - we tried.
Before giving the solution that now finally works, I first want to answer your questions @cosmicc.
If I understand correctly you’re proposing a MAP guide instead of the full posteriors? Is it the same as performing an AutoDelta guide?
A short answer to your question: Yes, AutoDelta should in principle equal a more or less “automated” MAP inference approach.
A more detailed answer: In above @fehiepsi 's post from Feb 2, he has given a “manual” MAP inference. What AutoDelta basically tries to achieve is a point estimate which is exactly what MAP inference basically is and what @fehiepsi has implemented. The reason why we additionally tried inference using the AutoDelta guide is because we combined it with an initialization process as described in the GMM example.
Unfortunately though, both methods did not yield satisfying inference results.
Why isn’t enumeration possible and how do I instead infer the latent states of the categorical distribution?
This is a very good question! In general, enumeration seems to be the most natural way to go for discrete latent variables in this case. However, we came across two major problems:
First, enumeration only supports a limited dimensionality, that is if you want to enumerate more than 25 variables, you have to apply some tricks. You can check the documentation for this provided here. As we wish to apply the SBM model for a larger-scale use case, this seems to be a more or less significant constraint w.r.t. plates parallelization, etc. where we are not sure how this would affect computation times and other things for our intended use-case.
Second, when using enumeration, indexing works a bit different. And this is exactly where we encountered most of the problems that subsequently affected other things in our code. In the definition of our adjacency matrix in the model, we are basically forced to use Vindex (don’t worry, this is also explained in above documentation link). To make it short, this led to some various problems regarding inference using our specified guide.
Current Solution
When we started looking for a probabilistic framework in order to implement the SBM, we wished for a very simple, easy to understand solution that relied on already existing widely used frameworks such as TensorFlow and PyTorch. Initially, Pyro seemed to provide all that and above all a very detailed documentation with many examples. However, for above stated reasons, the implementation of a simple Stochastic Block Model just would not work. I would not say that it is not possible as there are surely some variants and functionalities that are not explicitly detailed in the documentation, however after reviewing with @fehiepsi we now obtained an MCMC solution using a DiscreteHMCGibbs kernel. Please note that this exact implementation solution is not part of Pyro but of NumPyro. It works well, is very fast and most importantly correctly identifies memberships without any “good guess initializations”. Also note that NumPyro builds up on Google JAX which you have at least heard of recently if you are somewhat up to date with ML frameworks. As such, I would suggest to catch up on MCMC and HMC concepts in Pyro and then move on to NumPyro for the SBM realization.
Working SBM Example:
import jax
import jax.numpy as jnp
import numpyro
import numpyro.distributions as dist
from numpyro.infer import DiscreteHMCGibbs, MCMC, NUTS
import networkx as nx # Version 1.9.1
from observations import karate
import matplotlib.pyplot as plt
def model(A, K):
# Network Nodes
n = A.shape[0]
# Block Matrix Eta
with numpyro.plate("eta1", K):
with numpyro.plate("eta2", K):
eta = numpyro.sample("eta", dist.Beta(1., 1.))
# Group Memberships (Using a Multinomial Model)
membership_probs = numpyro.sample("z_probs", dist.Dirichlet(concentration=jnp.ones(K)))
with numpyro.plate("membership", n):
sampled_memberships = numpyro.sample("sampled_z", dist.Categorical(probs=membership_probs))
sampled_memberships = jax.nn.one_hot(sampled_memberships, K)
# Adjacency Matrix
p = jnp.matmul(jnp.matmul(sampled_memberships, eta), sampled_memberships.T)
with numpyro.plate("rows", n):
with numpyro.plate("cols", n):
A_hat = numpyro.sample("A_hat", dist.Bernoulli(p), obs=A)
# Simple Toy Data
A = jnp.array([
[0, 1, 1, 1, 1, 0, 0, 0, 0, 0],
[1, 0, 1, 1, 1, 0, 0, 0, 0, 0],
[1, 1, 0, 1, 1, 0, 0, 0, 0, 0],
[1, 1, 1, 0, 1, 0, 0, 0, 0, 0],
[1, 1, 1, 1, 0, 1, 0, 0, 0, 0],
[0, 0, 0, 0, 1, 0, 1, 1, 1, 1],
[0, 0, 0, 0, 0, 1, 0, 1, 1, 1],
[0, 0, 0, 0, 0, 1, 1, 0, 1, 1],
[0, 0, 0, 0, 0, 1, 1, 1, 0, 1],
[0, 0, 0, 0, 0, 1, 1, 1, 1, 0]])
Z = jnp.array([0, 0, 0, 0, 0, 1, 1, 1, 1, 1])
K = 2
# Inference
kernel = DiscreteHMCGibbs(NUTS(model))
mcmc = MCMC(kernel, num_warmup=1500, num_samples=2500)
mcmc.run(jax.random.PRNGKey(0), A, K)
mcmc.print_summary()
Z_infer = mcmc.get_samples()["sampled_z"]
Z_infer = Z_infer[-1]
print("Inference Result", Z_infer)
print("Original Memberships", Z)
# Visualization
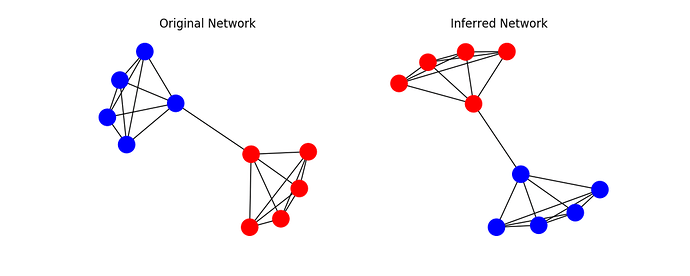
G = nx.from_numpy_matrix(A)
plt.figure(figsize=(10,4))
plt.subplot(121)
nx.draw(G, pos=nx.spring_layout(G), node_color=["red" if x==1 else "blue" for x in Z])
plt.title("Original Network")
plt.subplot(122)
nx.draw(G, pos=nx.spring_layout(G), node_color=["red" if x==1 else "blue" for x in Z_infer])
plt.title("Inferred Network")
plt.show()
We obtain the following result:
sample: 100%|██████████| 2000/2000 [00:15<00:00, 131.59it/s, 7 steps of size 5.16e-01. acc. prob=0.89]
mean std median 5.0% 95.0% n_eff r_hat
eta[0,0] 0.78 0.07 0.79 0.65 0.89 1524.15 1.00
eta[0,1] 0.07 0.05 0.06 0.00 0.14 1365.40 1.00
eta[1,0] 0.07 0.05 0.06 0.00 0.15 1937.00 1.00
eta[1,1] 0.78 0.08 0.79 0.66 0.90 1841.28 1.00
sampled_z[0] 0.00 0.00 0.00 0.00 0.00 nan nan
sampled_z[1] 0.00 0.00 0.00 0.00 0.00 nan nan
sampled_z[2] 0.00 0.00 0.00 0.00 0.00 nan nan
sampled_z[3] 0.00 0.00 0.00 0.00 0.00 nan nan
sampled_z[4] 0.00 0.00 0.00 0.00 0.00 nan nan
sampled_z[5] 1.00 0.00 1.00 1.00 1.00 nan nan
sampled_z[6] 1.00 0.00 1.00 1.00 1.00 nan nan
sampled_z[7] 1.00 0.00 1.00 1.00 1.00 nan nan
sampled_z[8] 1.00 0.00 1.00 1.00 1.00 nan nan
sampled_z[9] 1.00 0.00 1.00 1.00 1.00 nan nan
z_probs[0,0] 0.67 0.23 0.70 0.33 1.00 1785.41 1.00
z_probs[0,1] 0.33 0.23 0.30 0.00 0.67 1785.41 1.00
z_probs[1,0] 0.66 0.24 0.71 0.31 1.00 1393.45 1.00
z_probs[1,1] 0.34 0.24 0.29 0.00 0.69 1393.45 1.00
z_probs[2,0] 0.67 0.25 0.72 0.31 1.00 2086.85 1.00
z_probs[2,1] 0.33 0.25 0.28 0.00 0.69 2086.85 1.00
z_probs[3,0] 0.67 0.24 0.71 0.32 1.00 1866.58 1.00
z_probs[3,1] 0.33 0.24 0.29 0.00 0.68 1866.58 1.00
z_probs[4,0] 0.67 0.23 0.71 0.34 1.00 1572.49 1.00
z_probs[4,1] 0.33 0.23 0.29 0.00 0.66 1572.49 1.00
z_probs[5,0] 0.33 0.24 0.29 0.00 0.69 1532.02 1.00
z_probs[5,1] 0.67 0.24 0.71 0.31 1.00 1532.02 1.00
z_probs[6,0] 0.35 0.24 0.32 0.00 0.70 2433.68 1.00
z_probs[6,1] 0.65 0.24 0.68 0.30 1.00 2433.68 1.00
z_probs[7,0] 0.33 0.24 0.29 0.00 0.69 1966.93 1.00
z_probs[7,1] 0.67 0.24 0.71 0.31 1.00 1966.93 1.00
z_probs[8,0] 0.33 0.24 0.29 0.00 0.68 1725.91 1.00
z_probs[8,1] 0.67 0.24 0.71 0.32 1.00 1725.91 1.00
z_probs[9,0] 0.33 0.23 0.30 0.00 0.66 1216.91 1.00
z_probs[9,1] 0.67 0.23 0.70 0.34 1.00 1216.91 1.00
Inference Result [1 1 1 1 1 0 0 0 0 0]
Original Memberships [0 0 0 0 0 1 1 1 1 1]
Please Note:
SBM models - or at least in the current implementation provided here - are prone to two things: Label-Switching and Higher-Lower-Splits. As you can see, the labels are switched in this case which is not a problem at all. However, once you try to apply the solution to the Karate Club, you have to deal with higher and lower splittings, that is the model prefers nodes of higher degree over lower ones and thus constructs the groups as such. This is widely known and I suggest to read more on that on page 21 of this document.
I would like to thank @fehiepsi very much for his hugely appreciated help! We gained more insight into the Pyro mechanics and the solution we obtained together is pretty satisfying for our current use-case 
If there are any more questions, I am open to discuss them. For now, I hope the NumPyro solution works for you, too @cosmicc.
![]()
![]()