Spline Regression in Pyro (based on PyMC3 implementation)

Misc.
1

Hello,

TL;DR: I have a model that work with PyMC3 that I want to refactor to Pyro but the Pyro implementation is quite off compared to the PyMC3 one.

Background

I have been working on a model based on spline regression that I have implemented in PyMC3 and I would like to re-implement it in Pyro for scalability and also to evolve it. Basically I have different classes c (that I know) and for each classes I have a sequence of (x, y) that I am modelling using a spline regression as follow:

import pymc3 as pm
import scipy as sp 
from theano import shared

# dummy data:
n = 100
def foo(x):
    return np.sin(x * np.pi) + np.sin(x * np.pi * 2)

x = np.random.uniform(size = n)
e = np.random.normal(0, .1, n)
y = foo(x) + e

# spline regressors:
N_KNOT = 10
knots = np.linspace(0, 1, N_KNOT)
basis_funcs = sp.interpolate.BSpline(knots, np.eye(N_KNOT), k=1) # first order splines
trend_x = basis_funcs(x)

# PyMC3 model for a single class
trend_x_ = shared(trend_x)
n_ts = trend_x.shape[1]
with pm.Model() as model_spline:
    σ_a = pm.HalfCauchy('σ_a', 5.)
    a0 = pm.Normal('a0', 0., 10.)
    Δ_a = pm.Normal('Δ_a', 0., 1., shape=n_ts)
    a = pm.Deterministic('a', a0 + (σ_a * Δ_a).cumsum())
    
    mu = trend_x_.dot(a) 
    σ = pm.HalfCauchy('σ', 5.)
    obs = pm.Normal('obs', mu = mu, sd = σ, observed=y)
    
with model_spline:
    inference_spline = pm.ADVI()
    approx_spline = pm.fit(n=25000, method=inference_spline)
    trace_spline = approx_spline.sample(draws=1000)

And for the dummy data, the results are quite fitting:

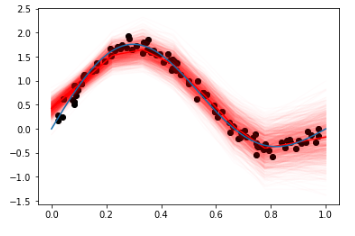
Pyro implementation

To simplify the management of the different classes, I wanted to leverage the Embedding layer and I replicated the implementation of the spline regression in PyMC3 in Pytorch:

import torch
import torch.nn as nn
from torch.autograd import Variable

class SplineRegression(nn.Module):
    def __init__(self, n_nodes, n_classes):
        super(SplineRegression, self).__init__()
        
        self.n_nodes = n_nodes
        self.n_classes = n_classes
        
        self.σ_a = nn.Embedding(self.n_classes, 1)
        self.Δ_a = nn.Embedding(self.n_classes, self.n_nodes)
        self.a0 = nn.Embedding(self.n_classes, 1)
        self.σ = nn.Embedding(self.n_classes, 1)
        
    def forward(self, c, t):
        a0 = self.a0(c)   # <- retrieve the value for the corresponding class/category
        Δ_a = self.Δ_a(c) # <- retrieve the values for the corresponding class/category
        σ_a = self.σ_a(c) # <- retrieve the value for the corresponding class/category
        σ = self.σ(c)     # <- retrieve the value for the corresponding class/category
        a = torch.cumsum(Δ_a, 1).mul(σ_a.reshape(-1, 1)) + a0         
        return torch.sum(t * a, 1).reshape(-1, 1), σ.reshape(-1, 1)

And I then created a Bayesian implementation with “lifted” modules, trying to use the same distributions as in the PyMC3 implementation:

import pyro
import pyro.distributions as dist
from pyro.infer import SVI, Trace_ELBO
from pyro.optim import Adam

class BayesianSplineRegression(nn.Module):
    def __init__(self, n_nodes, n_classes):
        super(BayesianSplineRegression, self).__init__()
        self.regression = SplineRegression(n_nodes, n_classes)

        self.n_nodes = n_nodes
        self.n_classes = n_classes
        
        pyro.clear_param_store()
        
    def model(self, c, t, y):
        σ_a_prior = dist.HalfCauchy(Variable(5. * torch.ones(self.n_classes, 1)))
        σ_prior = dist.HalfCauchy(Variable(5. * torch.ones(self.n_classes, 1)))
        
        Δ_a_prior = dist.Normal(
            Variable(torch.zeros(self.n_classes, self.n_nodes)),
            Variable(torch.ones(self.n_classes, self.n_nodes))
        )
        
        a0_prior = dist.Normal(
            Variable(torch.zeros(self.n_classes, 1)),
            Variable(10.*torch.ones(self.n_classes, 1))
        )
        
        priors = {
            'σ_a.weight': σ_a_prior.to_event(2),
            'Δ_a.weight': Δ_a_prior.to_event(2),
            'a0.weight': a0_prior.to_event(2),
            'σ.weight': σ_prior.to_event(2),
        }
        
        lifted_module = pyro.random_module("regression", self.regression, priors)
        lifted_regression = lifted_module()
        with pyro.plate("map", len(c)):
            mu, sig = lifted_regression(c, t)
            pyro.sample("obs", dist.Normal(mu, sig).to_event(2), obs=y)
        return mu, sig
    
    def guide(self, c=None, t=None, y=None):
        a0_loc = pyro.param('a0_loc', torch.zeros(self.n_classes, 1))
        a0_scale = pyro.param('a0_scale', torch.ones(self.n_classes, 1), constraint=constraints.positive)
        
        σ_a_loc = pyro.param('σ_a_loc', torch.ones(self.n_classes, 1), constraint=constraints.positive)
        σ_loc = pyro.param('σ_loc', torch.ones(self.n_classes, 1), constraint=constraints.positive)
        
        Δ_a_loc = pyro.param('Δ_a_loc', torch.zeros(self.n_classes, self.n_nodes))
        Δ_a_scale = pyro.param('Δ_a_scale', torch.ones(self.n_classes, self.n_nodes), constraint=constraints.positive)
        
        σ_a = dist.HalfCauchy(σ_a_loc)
        σ = dist.HalfCauchy(σ_loc)
        
        a0 = dist.Normal(a0_loc, a0_scale)
        Δ_a = dist.Normal(Δ_a_loc, Δ_a_scale)

        dists = {
            'σ_a.weight': σ_a.to_event(2),
            'Δ_a.weight': Δ_a.to_event(2),
            'a0.weight': a0.to_event(2),
            'σ.weight': σ.to_event(2),
        }
        lifted_module = pyro.random_module("regression", self.regression, dists)
        return lifted_module()
    
    def fit(self, c, t, y, lr=0.001, n_iter=10):
        pyro.clear_param_store()
        optim = Adam({"lr": lr})
        elbo = Trace_ELBO()
        self.svi = SVI(self.model, self.guide, optim, loss=elbo)
        losses = []
        for i in range(n_iter):
            losses.append(self.svi.step(c, t, y)/len(c))
        return losses

then, fit:

c_tch = torch.LongTensor([0]*n)
t_tch = torch.Tensor(trend_x)
y_tch = torch.Tensor(y)

model = BayesianSplineRegression(n_ts, 1)
losses = model.fit(c_tch, t_tch, y_tch, lr=0.1, n_iter=25000)

I then try to look at the fitted results by sampling models:

x_plot = np.linspace(0, 1, 299)
t_tch_pred = torch.FloatTensor(basis_funcs(x_plot))
c_tch_pred = torch.LongTensor([0]*x_plot.shape[0])

M = np.zeros((1000, len(x_plot)))
for i in range(1000):
    m_, _ = model.guide()(c_tch_pred, t_tch_pred)
    m_ = m_.detach().cpu().numpy().ravel()
    M[i,:] = m_
    plt.plot(x_plot, m_, alpha=.01, c='red')

plt.plot(x_plot, M.mean(0), c='red')
plt.plot(x_plot, foo(x_plot))
plt.scatter(x, y, c='black');

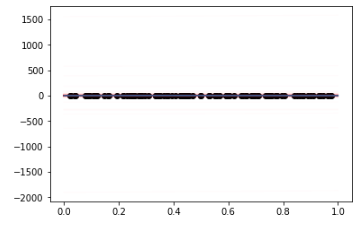
And the results is quite different from my other implementation. I am wondering whether I have a problem with the implementation of the guide function and I have tried to use the auto-guide function like AutoDiagonalNormal but I also get odd results. Any ideas on what I might have done wrong?

Thanks in advance!

2

i’m not familiar with how advi is implemented in pymc3, but it would be worth printing out the parameters learned in pymc3 vs the parameters learned in your pyro model. VI is sensitive to initialization so i’d recommend playing around with your initializations. for example, your guide std devs seem quite large given your data.

aside: if you are using pytorch > 0.3, you don’t need Variables.

3

Thanks @jpchen for your reply.
I actually took a step back and realised that I was mixing the prediction logic and my prior in SplineRegression. Basically, to smooth the coefficients of my regression I wanted to use a gaussian random walk to set the priors and instead of just implementing the weight and setting the priors to the random walk, I was writing the random walk logic in my regression.

In the end, I have simplified both python classes and managed to get it to work this way (thanks to @fehiepsi for the GaussianRandomWalk class I could borrow from there):

class SplineRegression(nn.Module):
    def __init__(self, n_nodes, n_groups):
        super(SplineRegression, self).__init__()
        
        self.n_nodes = n_nodes
        self.n_groups = n_groups
        self.alphas = nn.Embedding(n_groups, n_nodes)
        
    def forward(self, t, c):
        alphas = self.alphas(c)
        return torch.bmm(t.unsqueeze(1), alphas.unsqueeze(2)).squeeze()

class BayesianSplineRegression(nn.Module):
    def __init__(self, n_nodes, n_groups):
        super(BayesianSplineRegression, self).__init__()
        self.regression = SplineRegression(n_nodes, n_groups)
        self.n_nodes = n_nodes        
        self.n_groups = n_groups        
        pyro.clear_param_store()
        
    def _set_w_reg(self, w):
        self.regression.alphas.weight.data = w
    
    def sample(self, t, c, n=1):
        X = np.empty((n, len(t)))
        for i in range(n):
            w_dict = self.guide()
            self._set_w_reg(w_dict['module$$$alphas.weight'])
            y = self.regression(t, c).detach().cpu().numpy()
            X[i, :] = y.ravel()
        return X
    
    def model(self, t, y, c):
        n_groups, n_nodes = self.n_groups, self.n_nodes
        
#         w_prior = dist.Normal(torch.zeros(n_groups, n_nodes), torch.ones(n_groups, n_nodes)).to_event(1)
        scale_a = pyro.sample("sigma_a", dist.HalfCauchy(5.*torch.ones(n_groups)))
        w_prior = GaussianRandomWalk(scale_a, n_nodes).to_event(1)
        
        priors = {'alphas.weight': w_prior}
        scale = pyro.sample("sigma", dist.HalfCauchy(5.))
        # lift module parameters to random variables sampled from the priors
        lifted_module = pyro.random_module("module", self.regression, priors)
        # sample a nn (which also samples w and b)
        lifted_reg_model = lifted_module()
        with pyro.plate("map", len(t)):
            # run the nn forward on data
            prediction_mean = lifted_reg_model(t, c).squeeze(-1)
            # condition on the observed data
            pyro.sample("obs",
                        dist.Normal(prediction_mean, scale),
                        obs=y)
            return prediction_mean
    
    def fit(self, c, t, y, lr=.001, n_iter=10):
        pyro.clear_param_store()
        
        self.guide = AutoDiagonalNormal(self.model)
        optim = Adam({"lr": lr})
        elbo = Trace_ELBO()
        self.svi = SVI(self.model, self.guide, optim, loss=elbo)
        losses = []
        for j in range(n_iter):
            loss = self.svi.step(t, y, c)
            if j % 250 == 0:
                print("[iteration %04d] loss: %.4f" % (j + 1, loss / len(t)))
            losses.append(loss / len(t))
            
        return losses

This also could be used more generally to create conditional regressions based on the input c.

Again, thanks a lot @jpchen

3 Likes