I am attempting to model timeseries data from a physical system with a number of operating states; in each operating state, the evolution of the latent states will follow a different structure. We’re taking a markov switching approach, based loosely off the HMM enumeration tutorial (although we have continuous latent state, in comparison to the categorical y in the tutorial).
We seem to be getting an issue with dimensions being added to the state in the scan carry with each draw/iteration, as we see errors of this type:
TypeError: reshape total size must be unchanged, got new_sizes (2,) for shape (2, 2).
As far as we can see, each iteration seems to increase the dimension (and length?) of the elements we carry in the scan.
Any suggestions for how to handle this error?
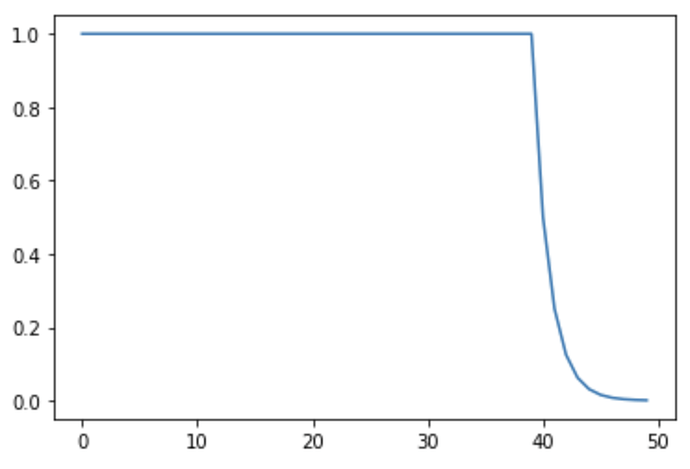
A toy example which generates the error above
We have a system in which the value of y does not change in state 0, and in state 1 the value of y is half of the previous value. Our state switches from 0 to 1 after 40 observations:
# pip install numpyro funsor
import numpyro
from numpyro.infer import MCMC, NUTS, Predictive
from numpyro.diagnostics import summary
from numpyro import distributions as dist
from numpyro.contrib.control_flow import scan, cond
from jax import random
import jax.numpy as jnp
import numpy as np
# create data:
y = np.ones(50)
for i in range(40,len(y)):
y[i] = y[i-1]*0.5
Define the model:
def model(dim_s,
dim_states,
y,
meas_err,
):
with numpyro.plate("x_plate", 1):
probs_x = numpyro.sample(
"probs_x", dist.Dirichlet(0.9 * jnp.eye(dim_states) + 0.1)
)
def transition(state,t):
x_prev, latent_prev = state
# draw the state:
x = numpyro.sample(
"x",
dist.Categorical(probs_x[x_prev]),
infer={"enumerate": "parallel"},
)
# squeeze to try to remove unnecessary dimensions?
x = x.squeeze()
# calculate evolution of latent state in each state:
latent_ = jnp.array([latent_prev, 0.5*latent_prev])
# based on state x, select update to latent state:
latent = latent_[x]
# observation equation:
y_obs = numpyro.sample("y_obs", dist.Normal(latent, meas_err), obs=y[t])
return (x, latent), (x, latent)
# uninformative initial priors:
y_init = numpyro.sample("y_init", dist.Normal(0,5))
x_init = numpyro.sample("x_init", dist.Categorical(jnp.array([0.5, 0.5])),
infer={'enumerate': 'parallel'})
_, states = scan(transition, (x_init, y_init), np.arange(dim_s))
return
Define model inputs and run:
prior = {"meas_err": 1,
"dim_s": len(y),
"dim_states": 2,
"y": jnp.asarray(y),}
ns = 1000
kernel = NUTS(model)
mcmc = MCMC(kernel, num_warmup=ns, num_samples=ns)
mcmc.run(random.PRNGKey(0), **prior, )