Let’s say I have the following graphical model
And I want to characterize the posterior of shift i for all i.
shift i are all scalars, particle i is a vector (e.g. N=64), with iid Gaussian noise in each element.
How do I take advantage of the vectorization of pyro.plate?
If num particles is very large (10k - 1 million), will it be prohibitively slow to name all of the shifts?
If your number of particles is too large to fit in memory, you could amortize by inferring a posterior distribution of shift[i] as a function of local data particle[i]. For example let’s say you’ve defined a multilayer perceptron mlp that inputs a batch of particles and outputs a pair of batched loc, scale parameters. Then your model and guide could look like
def model(data, full_size=None):
if full_size is None:
full_size = len(data)
with pyro.plate("data", full_size, subsample=data):
pyro.sample("shift", dist.Normal(0, 1))
pyro.sample("particle", dist.Normal(shift, 1), obs=data)
def guide(data, full_size=None):
if full_size is None:
full_size = len(data)
pyro.module("mlp", mlp)
with pyro.plate("data", full_size, subsample=data):
loc, scale = mlp(data)
pyro.sample("shift", dist.Normal(loc, scale))
you’d then train the guide by passing in minibatches of data, together with the full data size.
Thanks this is very helpful, and was suggested by my course instructor. Thanks very much for the code snippet. Nice to see how I don’t need to name the different shifts different names, because the guide sees the data, and predicts the shift loc and scale from the data.
Thanks again. I got something working with amortization here. It just takes in one particle at a time, but I’ll try to extend it to minibatches of data.
The model is
def model(one_particle):
shift = pyro.sample("shift", dist.Normal(0, 2))
clean_signal = torch.exp(-(domain-shift)**2/(2*sigma_signal_gt**2))
with pyro.plate('data',num_pix):
pyro.sample("particle", dist.Normal(clean_signal, sigma_noise).to_event(1), obs=one_particle)
So do I understand things right in that the data plate with pyro.plate('data',num_pix=32) and .to_event(1) and obs=one_particle is how to tell pyro that the noise added to the clean measurement is iid?
I will try to extend to minibatches of particles with another plate as in your code snippet.
Am I going about this the right way?
num_pix=64)mini_batch plate gives shifts of the size of the mini batchThere’s no errors, but I’m not sure I’m using the plates in the right way. The mlp doesn’t train well at all (batch sizes 1, 2, 10, etc). I think I’m training enough since the same problem with out the mini batches and feeding in one example is working (seeing all 1000 examples 10 times each)
mlp = MLP()
def model(mini_batch):
full_size = len(mini_batch)
with pyro.plate('mini_batch',full_size,subsample=mini_batch):
shift = pyro.sample("shift", dist.Normal(0, 2)) # mini batch of different shifts, of size defined by size in pyro.plate(..., size)
clean_signal = torch.exp(-(domain.reshape(1,-1)-shift.reshape(full_size,1))**2/(2*sigma_signal_gt**2)) # mini batch of clean signals, representing a mini batch of noiseless, but shifted particles
with pyro.plate('pixels',num_pix):
pyro.sample("particle", dist.Normal(clean_signal, sigma_noise).to_event(1), obs=mini_batch) # upon each of these noiseless, shifted particles, gaussian noise is added
def guide(mini_batch): # the proposal distribution
"""
mlp will be trained on many particles to predict params of distribution
"""
full_size = len(mini_batch)
pyro.module("mlp", mlp)
with pyro.plate('mini_batch', full_size, subsample=mini_batch):
loc, log_scale = mlp(one_particle)
scale = torch.exp(log_scale)
pyro.sample("shift", dist.Normal(loc, scale))
pyro.clear_param_store()
svi = pyro.infer.SVI(model=model,
guide=guide,
optim=pyro.optim.Adam({"lr": 0.03}),
loss=pyro.infer.Trace_ELBO())
losses = []
n_epochs = 10
batch_size = 10
for t in range(n_epochs):
random_idx = torch.randperm(num_particles)
permutation = data.index_select(0,random_idx)
for i in range(0,len(data), batch_size):
mini_batch = permutation[i:i+batch_size]
losses.append(svi.step(mini_batch))
Yes, your pyro.plate("data") declares that noise is iid over particles. If you believe noise is also iid over pixels you could replace the .to_event(1) with a pyro.plate("pixels"). In your last reply, you should omit .to_even(1) and explicitly specify the dim of each plate:
with pyro.plate('mini_batch',full_size,subsample=mini_batch, dim=-2):
...
with pyro.plate('pixels',num_pix, dim=-1):
...
(otherwise dims will be allocated automatically, and end up reversed, with the data plate to the right of the pixels plate)
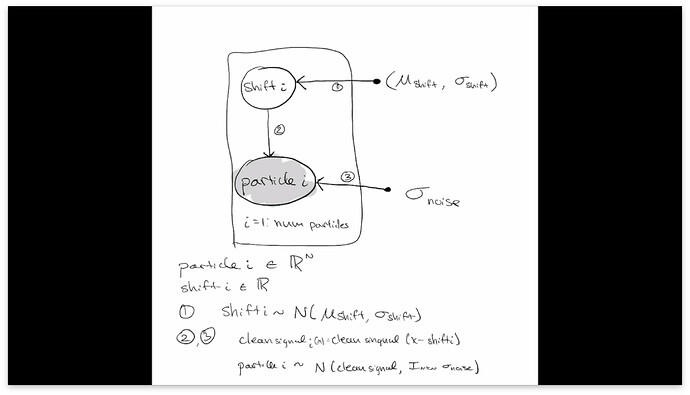
Ok I got the mini batches working with to_event. Predictions match the gt, so the amortization is working: prob_prog/pyro_1D_shift_amortized.ipynb at main · geoffwoollard/prob_prog · GitHub
The issue was a bug in my guide, which was using the wrong data (mlp(one_particle) → mlp(mini_batch))
I like the dim option in pyro.plate. I tried to get that working, but there was some issue with the sizes of shift being (mini_batch,1) in the model vs mini_batch in the guide.
Here we see things working fine with .to_event(1)
mlp = MLP()
do_log=True
def model(mini_batch):
full_size = len(mini_batch)
with pyro.plate('mini_batch',full_size,subsample=mini_batch):
shift = pyro.sample("shift", dist.Normal(0, 2)) # mini batch of different shifts, of size defined by size in pyro.plate(..., size)
if do_log: print('model shift.shape',shift.shape)
if do_log: print('model shift',shift)
clean_signal = torch.exp(-(domain.reshape(1,-1)-shift.reshape(full_size,1))**2/(2*sigma_signal_gt**2)) # mini batch of clean signals, representing a mini batch of noiseless, but shifted particles
if do_log: print('model clean_signal.shape',clean_signal.shape)
with pyro.plate('pixels',num_pix):
distrib = dist.Normal(clean_signal, sigma_noise)
if do_log: print('model particle normal',distrib)
pyro.sample("particle", distrib.to_event(1), obs=mini_batch) # upon each of these noiseless, shifted particles, gaussian noise is added
def guide(mini_batch): # the proposal distribution
"""
mlp will be trained on many particles to predict params of distribution
"""
full_size = len(mini_batch)
pyro.module("mlp", mlp)
with pyro.plate('mini_batch', full_size, subsample=mini_batch):
lam = mlp(mini_batch)
loc, log_scale = lam[:,0], lam[:,1]
scale = torch.exp(log_scale)
distrib = dist.Normal(loc, scale)
if do_log: print('guide shift normal',distrib)
pyro.sample("shift", distrib)
pyro.clear_param_store()
svi = pyro.infer.SVI(model=model,
guide=guide,
optim=pyro.optim.Adam({"lr": 0.03}),
loss=pyro.infer.Trace_ELBO())
losses = []
n_epochs = 1
batch_size = 2
epoch_size = 4#len(data)
for t in range(n_epochs):
random_idx = torch.randperm(num_particles)
permutation = data.index_select(0,random_idx)
for i in range(0,epoch_size, batch_size):
mini_batch = permutation[i:i+batch_size]
losses.append(svi.step(mini_batch))
# guide shift normal Normal(loc: torch.Size([2]), scale: torch.Size([2]))
# model shift.shape torch.Size([2])
# model shift tensor([-0.2310, -0.3911], grad_fn=<AddBackward0>)
# model clean_signal.shape torch.Size([2, 32])
# model particle normal Normal(loc: torch.Size([2, 32]), scale: torch.Size([2, 32]))
# guide shift normal Normal(loc: torch.Size([2]), scale: torch.Size([2]))
# model shift.shape torch.Size([2])
# model shift tensor([1.2149, 0.1887], grad_fn=<AddBackward0>)
# model clean_signal.shape torch.Size([2, 32])
# model particle normal Normal(loc: torch.Size([2, 32]), scale: torch.Size([2, 32]))
And below is the errors I’m seeing with dim in the plates
(input)
mlp = MLP()
do_log=True
def model(mini_batch):
full_size = len(mini_batch)
with pyro.plate('mini_batch',full_size,subsample=mini_batch,dim=-2):
shift = pyro.sample("shift", dist.Normal(0, 2)) # mini batch of different shifts, of size defined by size in pyro.plate(..., size)
if do_log: print('model shift.shape',shift.shape)
if do_log: print('model shift',shift)
clean_signal = torch.exp(-(domain.reshape(1,-1)-shift.reshape(full_size,1))**2/(2*sigma_signal_gt**2)) # mini batch of clean signals, representing a mini batch of noiseless, but shifted particles
if do_log: print('model clean_signal.shape',clean_signal.shape)
with pyro.plate('pixels',num_pix,dim=-1):
distrib = dist.Normal(clean_signal, sigma_noise)
if do_log: print('model particle normal',distrib)
pyro.sample("particle", distrib, obs=mini_batch) # upon each of these noiseless, shifted particles, gaussian noise is added
def guide(mini_batch): # the proposal distribution
"""
mlp will be trained on many particles to predict params of distribution
"""
full_size = len(mini_batch)
pyro.module("mlp", mlp)
with pyro.plate('mini_batch', full_size, subsample=mini_batch):
lam = mlp(mini_batch)
loc, log_scale = lam[:,0], lam[:,1]
scale = torch.exp(log_scale)
distrib = dist.Normal(loc, scale)
if do_log: print('guide shift normal',distrib)
pyro.sample("shift", distrib)
pyro.clear_param_store()
svi = pyro.infer.SVI(model=model,
guide=guide,
optim=pyro.optim.Adam({"lr": 0.03}),
loss=pyro.infer.Trace_ELBO())
losses = []
n_epochs = 1
batch_size = 2
epoch_size = 4#len(data)
for t in range(n_epochs):
random_idx = torch.randperm(num_particles)
permutation = data.index_select(0,random_idx)
for i in range(0,epoch_size, batch_size):
# https://stackoverflow.com/questions/45113245/how-to-get-mini-batches-in-pytorch-in-a-clean-and-efficient-way
mini_batch = permutation[i:i+batch_size]
losses.append(svi.step(mini_batch))
(errors)
guide shift normal Normal(loc: torch.Size([2]), scale: torch.Size([2]))
model shift.shape torch.Size([2])
model shift tensor([0.7913, 0.8643], grad_fn=<AddBackward0>)
model clean_signal.shape torch.Size([2, 32])
model particle normal Normal(loc: torch.Size([2, 32]), scale: torch.Size([2, 32]))
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
<ipython-input-229-8ff909300b55> in <module>()
47 # https://stackoverflow.com/questions/45113245/how-to-get-mini-batches-in-pytorch-in-a-clean-and-efficient-way
48 mini_batch = permutation[i:i+batch_size]
---> 49 losses.append(svi.step(mini_batch))
5 frames
/usr/local/lib/python3.7/dist-packages/pyro/util.py in check_model_guide_match(model_trace, guide_trace, max_plate_nesting)
339 raise ValueError(
340 "Model and guide shapes disagree at site '{}': {} vs {}".format(
--> 341 name, model_shape, guide_shape
342 )
343 )
ValueError: Model and guide shapes disagree at site 'shift': torch.Size([2, 1]) vs torch.Size([2])
Re: errors, I believe you’ll also need to specify dim=-2 in your guide’s plate.
Starting with the first plate at dim=-2, changes the shape to (3,1) and then it doesn’t match the guide, even when the plate in the guide also has dim=-2
I read through Tensor shapes in Pyro — Pyro Tutorials 1.8.4 documentation to understand better what’s happening with dim and nested plates. Rather that starting off with dim=-2, I just changed the shape of the mini batch, to match what happens in the model. It’s natural for me to start with a plate for measurements, then a plate for independent things that happen in that measurement, so I like it this way.
mlp = MLP()
do_log=False
def model(mini_batch):
"""
simulates a batch of particles, corresponding to observed mini_batch of particles
"""
full_size = len(mini_batch.T)
if do_log: print('full_size',full_size)
with pyro.plate('mini_batch',full_size, dim=-1):
shift = pyro.sample("shift", dist.Normal(0, 2)) # mini batch of different shifts, of size defined by size in pyro.plate(..., size)
# assert shift.shape == (3,1)
if do_log: print('model shift.shape',shift.shape)
if do_log: print('model shift',shift)
clean_signal = torch.exp(-(domain.reshape(1,-1)-shift.reshape(full_size,1))**2/(2*sigma_signal_gt**2)).T # mini batch of clean signals, representing a mini batch of noiseless, but shifted particles
if do_log: print('model clean_signal.shape',clean_signal.shape)
with pyro.plate('pixels',num_pix, dim=-2):
distrib = dist.Normal(clean_signal, sigma_noise)
if do_log: print('model particle normal',distrib)
if do_log: print('model mini_batch.T.shape',mini_batch.shape)
pyro.sample("particle", distrib, obs=mini_batch) # upon each of these noiseless, shifted particles, gaussian noise is added
model(mini_batch.T)
def guide(mini_batch): # the proposal distribution
"""
mlp will be trained on many particles to predict params of distribution
"""
full_size = len(mini_batch.T)
pyro.module("mlp", mlp)
with pyro.plate('mini_batch', full_size, dim=-1):
lam = mlp(mini_batch.T)
loc, log_scale = lam[:,0], lam[:,1]
scale = torch.exp(log_scale)
distrib = dist.Normal(loc, scale)
if do_log: print('guide shift normal',distrib)
pyro.sample("shift", distrib)
pyro.clear_param_store()
svi = pyro.infer.SVI(model=model,
guide=guide,
optim=pyro.optim.Adam({"lr": 0.03}),
loss=pyro.infer.Trace_ELBO())
losses = []
n_epochs = 5
batch_size = 25
epoch_size = len(data)
for t in range(n_epochs):
random_idx = torch.randperm(num_particles)
permutation = data.index_select(0,random_idx)
for i in range(0,epoch_size, batch_size):
mini_batch = permutation[i:i+batch_size]
losses.append(svi.step(mini_batch.T))