It is even simpler: 1 \times D \times 1.
Regarding your remark on the weights, I may have set a very small prior indeed, but increasing the scale does not really help.
I have done some tests, and came back to pyro (not numpyro) and found very different behavior which makes me think I have not done what I wanted with numpyro 
Below is the code for numpyro and pyro for a tiny BNN of size 1 \times 5 \times 1 with, in theory, the same prior for weights and biases (10.) and the same prior for the output scale (0.5). Number of parameters: N_{param}= (1\times 5) + 5 + (5 \times 1) + 1= 16 .
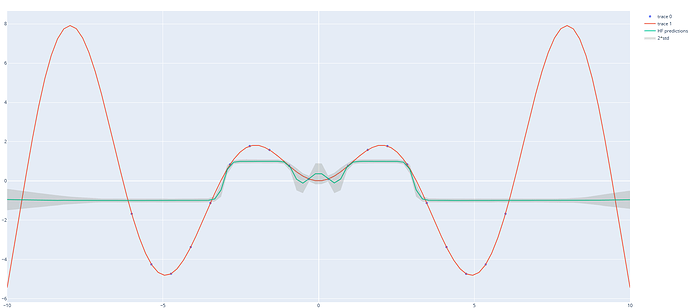
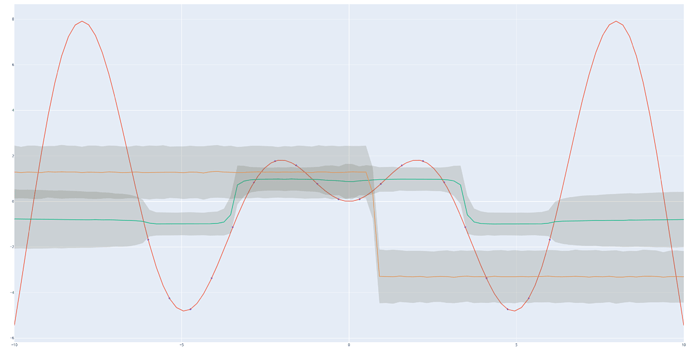
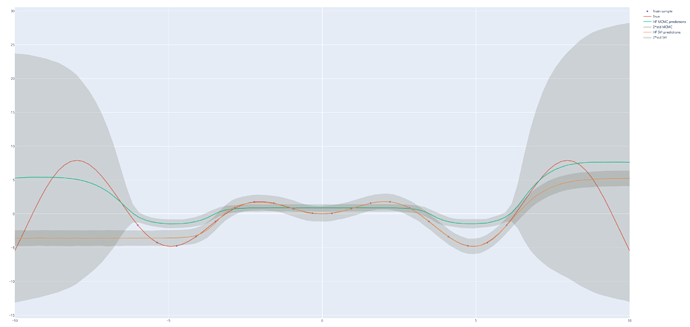
Although numpyro is much much faster, there is definitely something wrong compared to what pyro gives me, it is obvious for the MAP estimate, and less clear for the MCMC (with much less sample for pyro).
I will try next to initialize MCMC with MAP estimates. But in the meantime, any idea of what is going wrong with the numpyro model?
With numpyro:
With Pyro:
This is the code for numpyro for my simple test:
import jax.numpy as jnp
import jax.random as random
from jax import vmap
import numpy as np
import numpyro
from numpyro import handlers
import numpyro.distributions as distnumpyro
from numpyro.infer import MCMC as MCMCnumpyro
from numpyro.infer import NUTS as NUTSnumpyro
from numpyro.infer import Predictive as PredictiveNumpyro
import os
import time
import plotly.graph_objects as go
from collections import namedtuple
def model_bnn_numpyro(X, Y, hid_dim=5, out_dim=1, prior_scale=10.0, output_prior_scale=0.5):
N, D_X = X.shape
D_H = hid_dim
D_Y = out_dim
activation = jnp.tanh
# sample first layer (we put unit normal priors on all weights)
w1 = numpyro.sample("w1", distnumpyro.Normal(jnp.zeros((D_X, D_H)), jnp.ones((D_X, D_H)) * prior_scale).to_event(2))
b1 = numpyro.sample("b1", distnumpyro.Normal(jnp.zeros(D_H), jnp.ones(D_H) * prior_scale).to_event(1))
z1 = activation(jnp.matmul(X, w1) + b1) # <= first layer of activations
# sample final layer of weights and neural network output
w3 = numpyro.sample("w3", distnumpyro.Normal(jnp.zeros((D_H, D_Y)), jnp.ones((D_H, D_Y)) * prior_scale).to_event(2))
b3 = numpyro.sample("b3", distnumpyro.Normal(jnp.zeros(D_Y), jnp.ones(D_Y) * prior_scale).to_event(1))
z3 = activation(jnp.matmul(z1, w3) + b3) # <= output of the neural network
#prec_obs = numpyro.sample("prec_obs", distnumpyro.Gamma(3.0, 1.0))
#sigma_obs = 1.0 / jnp.sqrt(prec_obs)
# observe data
with numpyro.plate("data", N):
numpyro.sample("Y", distnumpyro.Normal(z3, output_prior_scale * output_prior_scale).to_event(1), obs=Y)
# helper function for HMC inference
def run_inference(model, args, rng_key, X, Y, D_H, prior_scale, output_prior_scale):
start = time.time()
kernel = NUTSnumpyro(model)
mcmc = MCMCnumpyro(
kernel,
num_warmup=args.num_warmup,
num_samples=args.num_samples,
num_chains=args.num_chains,
progress_bar=False if "NUMPYRO_SPHINXBUILD" in os.environ else True,
)
mcmc.run(rng_key, X, Y, D_H, prior_scale=prior_scale , output_prior_scale=output_prior_scale)
#mcmc.print_summary()
print("\nMCMC elapsed time:", time.time() - start)
return mcmc.get_samples(), mcmc
def run_vi(model, guide, n_steps, step_size, rng_key, X, Y, D_H, prior_scale, output_prior_scale):
adam = numpyro.optim.Adam(step_size=step_size)
elbo = numpyro.infer.Trace_ELBO(num_particles=1)
svi = numpyro.infer.SVI(model, guide, adam, elbo) # optimization variable are automatically inferred from guide definition
svi_result = svi.run(
rng_key=rng_key,
num_steps=n_steps,
X=X, Y=Y, hid_dim=D_H,
prior_scale=prior_scale, output_prior_scale=output_prior_scale
)
return svi_result
if __name__ == "__main__":
# Generate training and test data
x_train = np.linspace(0, 1, 20)
x_train = x_train * 12 - 6
y_train = x_train * np.sin(x_train)
x_test = x_test = np.linspace(0, 1, 100)
x_test = x_test * 20 - 10
y_test = x_test * np.sin(x_test)
d_input = [
go.Scatter(x=x_train, y=y_train, mode='markers', name='Train sample'),
go.Scatter(x=x_test, y=y_test, mode='lines', name='True')
]
N_neur = 5
prior_scale=10.0
output_prior_scale=0.5
# Variational Inference: MAP
autoguide = numpyro.infer.autoguide.AutoDelta(model_bnn_numpyro)
svi = run_vi(
model_bnn_numpyro,
autoguide,
50000,
1e-3,
random.PRNGKey(1),
x_train[:,np.newaxis],
( (y_train - y_train.mean()) / y_train.std() )[:,np.newaxis],
N_neur,
prior_scale,
output_prior_scale
)
# Get samples from approximate posterior
predictive = numpyro.infer.Predictive(model_bnn_numpyro, guide=autoguide, num_samples=2000)
svi_samples = predictive(random.PRNGKey(1), x_test[:,np.newaxis], Y=None, hid_dim=5, prior_scale=10.0, output_prior_scale=0.5)
samples_from_svi = svi_samples['Y'] * y_train.std() + y_train.mean()
mean_from_svi = samples_from_svi.mean(0).squeeze()
std_from_svi = samples_from_svi.std(0).squeeze()
yplus_from_svi = mean_from_svi + 2*std_from_svi
yminus_from_svi = mean_from_svi - 2*std_from_svi
# Sample via MCMC
rng_key, rng_key_predict = random.split(random.PRNGKey(0))
Args = namedtuple("args", "num_warmup num_samples num_chains")
args = Args(2000, 5000, 1)
samples, mcmc = run_inference(
model_bnn_numpyro,
args,
rng_key,
x_train[:,np.newaxis],
( (y_train - y_train.mean()) / y_train.std() )[:,np.newaxis],
N_neur,
prior_scale,
output_prior_scale
)
# Get the posterior samples
predictive = PredictiveNumpyro(model_bnn_numpyro, samples)
predictions = predictive(rng_key_predict, X=x_test[:,np.newaxis], Y=None, hid_dim=N_neur)['Y'].squeeze()
mean_prediction = jnp.mean(predictions, axis=0)
std_prediction = jnp.std(predictions, axis=0)
yplus = mean_prediction + 2*std_prediction
yminus = mean_prediction - 2*std_prediction
# Plot it
fig = go.Figure(
d_input + [
go.Scatter(x=x_test, y=mean_prediction, mode='lines', name='HF MCMC predictions'),
go.Scatter(
x=x_test.tolist() + x_test.tolist()[::-1], # x, then x reversed
y=yplus.tolist() + yminus.tolist()[::-1], # upper, then lower reversed
fill='toself',
fillcolor='rgba(100,100,80,0.2)',
line=dict(color='rgba(255,255,255,0)'),
hoverinfo="skip",
showlegend=True,
name='2*std MCMC'
),
go.Scatter(x=x_test, y=mean_from_svi, mode='lines', name='HF SVI predictions'),
go.Scatter(
x=x_test.tolist() + x_test.tolist()[::-1], # x, then x reversed
y=yplus_from_svi.tolist() + yminus_from_svi.tolist()[::-1], # upper, then lower reversed
fill='toself',
fillcolor='rgba(100,100,80,0.2)',
line=dict(color='rgba(255,255,255,0)'),
hoverinfo="skip",
showlegend=True,
name='2*std SVI'
)
]
)
fig.write_html('numpyro_simple_bnn.html')
And the same code for Pyro:
import numpy as np
import os
import time
import plotly.graph_objects as go
from collections import namedtuple
import torch
import pyro
import pyro.distributions as dist
from pyro.nn import PyroModule, PyroSample
import torch.nn as nn
from pyro.infer import MCMC, NUTS, Predictive
class OneHiddenLayerBNN(PyroModule):
def __init__(self, in_dim=1, out_dim=1, hid_dim=5, prior_scale=10., output_prior_scale=0.5):
super().__init__()
self.output_prior_scale = output_prior_scale
self.activation = nn.Tanh() # or ReLU()
self.layer1 = PyroModule[nn.Linear](in_dim, hid_dim)
self.layer2 = PyroModule[nn.Linear](hid_dim, out_dim)
# Set layer parameters as random variables
self.layer1.weight = PyroSample(dist.Normal(torch.tensor(0.), prior_scale).expand([hid_dim, in_dim]).to_event(2)) # Latent random variables
self.layer1.bias = PyroSample(dist.Normal(torch.tensor(0.,), prior_scale).expand([hid_dim]).to_event(1)) # Latent random variables
self.layer2.weight = PyroSample(dist.Normal(torch.tensor(0.), prior_scale).expand([out_dim, hid_dim]).to_event(2)) # Latent random variables
self.layer2.bias = PyroSample(dist.Normal(torch.tensor(0.), prior_scale).expand([out_dim]).to_event(1)) # Latent random variables
def forward(self, x, y=None):
x = x.reshape(-1, 1)
x = self.activation(self.layer1(x))
mu = self.layer2(x).squeeze()
#sigma = pyro.sample('sigma', dist.Gamma(torch.tensor(0.5, device="cuda"), 1.0)) # Infer response noise, Latent random variables
# Sampling model
with pyro.plate('data', x.shape[0]):
obs = pyro.sample('obs', dist.Normal(mu, self.output_prior_scale * self.output_prior_scale), obs=y) # observed variable
return mu
# helper function for HMC inference
def run_inference(model, args, X, Y):
start = time.time()
nuts_kernel = NUTS(model, jit_compile=True)
mcmc = MCMC(nuts_kernel, num_samples=args.num_samples, warmup_steps=args.num_warmup)
mcmc.run(X, Y)
print("\nMCMC elapsed time:", time.time() - start)
return mcmc.get_samples(), mcmc
def run_vi(model, guide, n_steps, step_size, X, Y):
pyro.clear_param_store() # reinit params
adam = pyro.optim.Adam({'lr': step_size}) # thin wrapper around pytorch adam, we could also give a function that returns parameters depending on parameter name (https://pyro.ai/examples/svi_part_i.html#Optimizers)
elbo = pyro.infer.Trace_ELBO(num_particles=1)
svi = pyro.infer.SVI(model, guide, adam, elbo) # optimization variable are automatically inferred from guide definition
losses = []
for step in range(n_steps):
loss = svi.step(X, Y) # takes a single gradient step and returns an estimate of the loss
losses.append(loss)
if step % 500 == 0:
print('Elbo loss: {}'.format(loss))
return svi
if __name__ == "__main__":
# Generate training and test data
x_train = np.linspace(0, 1, 20)
x_train = x_train * 12 - 6
y_train = x_train * np.sin(x_train)
x_test = x_test = np.linspace(0, 1, 100)
x_test = x_test * 20 - 10
y_test = x_test * np.sin(x_test)
d_input = [
go.Scatter(x=x_train, y=y_train, mode='markers', name='Train sample'),
go.Scatter(x=x_test, y=y_test, mode='lines', name='True')
]
torch.set_default_dtype(torch.float64)
xt = torch.from_numpy(x_train)
yt = torch.from_numpy(((y_train - y_train.mean()) / y_train.std()))
N_neur = 5
prior_scale=10.0
output_prior_scale=0.5
model = OneHiddenLayerBNN(hid_dim=N_neur, prior_scale=prior_scale, output_prior_scale=output_prior_scale)
# Variational Inference: MAP
autoguide = pyro.infer.autoguide.AutoDelta(model)
svi = run_vi(
model,
autoguide,
50000,
1e-3,
xt,
yt
)
# Get samples from approximate posterior
predictive = pyro.infer.Predictive(model, guide=autoguide, num_samples=2000)
# Second, run the model in forward using the guide samples instead of the 'a = pyro.sample('a', dist.Normal(0.0, 10.))" sample in the model
svi_samples = predictive(x=torch.from_numpy(x_test), y=None) # Must not provid the true y values
samples_from_svi = svi_samples['obs'] * y_train.std() + y_train.mean()
mean_from_svi = samples_from_svi.mean(0).squeeze()
std_from_svi = samples_from_svi.std(0).squeeze()
yplus_from_svi = mean_from_svi + 2*std_from_svi
yminus_from_svi = mean_from_svi - 2*std_from_svi
# Sample via MCMC
Args = namedtuple("args", "num_warmup num_samples num_chains")
#args = Args(2000, 5000, 1)
args = Args(100, 500, 1)
samples, mcmc = run_inference(
model,
args,
xt,
yt,
)
# Get the posterior samples
predictive = Predictive(model=model, posterior_samples=mcmc.get_samples())
predictions = predictive(x=torch.from_numpy(x_test), y=None)
mean_prediction = predictions['obs'].T.detach().cpu().numpy().mean(axis=1)
std_prediction = predictions['obs'].T.detach().cpu().numpy().std(axis=1)
yplus = mean_prediction + 2*std_prediction
yminus = mean_prediction - 2*std_prediction
# Plot it
fig = go.Figure(
d_input + [
go.Scatter(x=x_test, y=mean_prediction, mode='lines', name='HF MCMC predictions'),
go.Scatter(
x=x_test.tolist() + x_test.tolist()[::-1], # x, then x reversed
y=yplus.tolist() + yminus.tolist()[::-1], # upper, then lower reversed
fill='toself',
fillcolor='rgba(100,100,80,0.2)',
line=dict(color='rgba(255,255,255,0)'),
hoverinfo="skip",
showlegend=True,
name='2*std MCMC'
),
go.Scatter(x=x_test, y=mean_from_svi, mode='lines', name='HF SVI predictions'),
go.Scatter(
x=x_test.tolist() + x_test.tolist()[::-1], # x, then x reversed
y=yplus_from_svi.tolist() + yminus_from_svi.tolist()[::-1], # upper, then lower reversed
fill='toself',
fillcolor='rgba(100,100,80,0.2)',
line=dict(color='rgba(255,255,255,0)'),
hoverinfo="skip",
showlegend=True,
name='2*std SVI'
)
]
)
fig.write_html('pyro_simple_bnn.html')