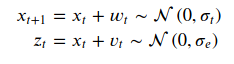Simple 1d filtering

1

Hello,
I tried to modify the Levy stable example to fit a simple 1d Kalman filter with the equations.
image
Actually my goal was to get started and to modify the observation variance with a NN based on the data input.

Here is the code:

 def model(data):
    x_0 = pyro.deterministic("x_0", data[0]).unsqueeze(-1)
    sigma = pyro.sample("sigma", dist.Normal(0, 1)).unsqueeze(-1)
    w = pyro.sample("w", dist.Normal(0, 1).expand(data.shape).to_event(1))
    x_t = pyro.deterministic("x_t", x_0 + sigma * w.cumsum(dim=-1))

    sigma_z = pyro.sample("sigma_z", dist.Normal(0, 1)).unsqueeze(-1)
    z_t = pyro.sample("z_t", dist.Normal(x_t, sigma_z).expand(data.shape).to_event(1), obs=data)

Training:

pyro.clear_param_store()
pyro.set_rng_seed(1234567890)
num_steps = 1 if smoke_test else 1001
optim = ClippedAdam({"lr": 0.05, "betas": (0.9, 0.99), "lrd": 0.1 ** (1 / num_steps)})
guide = AutoDiagonalNormal(model)
svi = SVI(model, guide, optim, Trace_ELBO())
for step in range(num_steps):
    loss = svi.step(r)

Based on my data I’m getting an nan in the loss. So guess something is really wrong. Thanks for any hint.

2

looks like you’re letting sigma_z be negative. it needs to be positive. perhaps use a LogNormal distribution?

3

Thanks a lot! Yes that helped : )
Now getting some reasonable results.

image

Guess will have to how to modify it a bit, to get the filtered process near the observation process.

4

Hello,
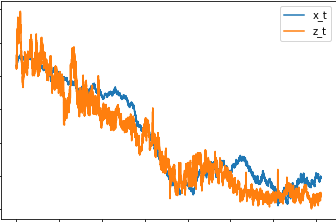
I tried to fix the model, but still getting a bit of confusing results. The fitted local level is kind of near the true value but still it should follow the time series much closer.
Not sure what is going wrong. The data size is big 19335 rows, maybe that is the problem. Any idea what is going wrong? Appreciate any help! Thanks

model

def model(data):
    x_0 = pyro.deterministic("x_0", data[0]).unsqueeze(-1)
    sigma = pyro.sample("sigma", dist.Uniform(0, 1e-3)).unsqueeze(-1)
    w = pyro.sample("w", dist.Normal(0, 1).expand(data.shape).to_event(1))
    x_t = pyro.deterministic("x_t", x_0 + sigma * w.cumsum(dim=-1))

    sigma_z = pyro.sample("sigma_z", dist.Uniform(0, 1e-3)).unsqueeze(-1)
    z_t = pyro.sample("z_t", dist.Normal(x_t, sigma_z).expand(data.shape).to_event(1), obs=data)

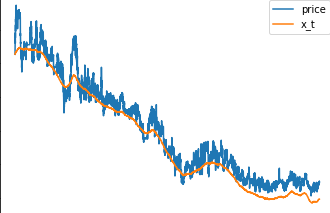
This is how the smoothed values x_t looks like

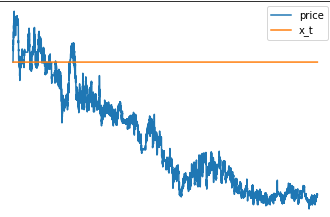
image

I was playing around with the model and tried to make the local level x_t only change its value in 90 % of the time. After training I got this results. Does overwriting some of the sampled values with zeros brakes the inference?

image

Here is the complete Code

imports

import pyro
from pyro.optim import ClippedAdam
from pyro.infer.autoguide import AutoDiagonalNormal
from pyro.infer import  SVI, Trace_ELBO, Predictive
import pandas as pd
import torch
import pyro.distributions as dist
from matplotlib import pyplot

model

def model(data):
    x_0 = pyro.deterministic("x_0", data[0]).unsqueeze(-1)
    sigma = pyro.sample("sigma", dist.Uniform(0, 1e-3)).unsqueeze(-1)
    w = pyro.sample("w", dist.Normal(0, 1).expand(data.shape).to_event(1))
    x_t = pyro.deterministic("x_t", x_0 + sigma * w.cumsum(dim=-1))

    sigma_z = pyro.sample("sigma_z", dist.Uniform(0, 1e-3)).unsqueeze(-1)
    z_t = pyro.sample("z_t", dist.Normal(x_t, sigma_z).expand(data.shape).to_event(1), obs=data)

# modified trend 
def model2(data):
    x_0 = pyro.deterministic("x_0", data[0]).unsqueeze(-1)
    sigma = pyro.sample("sigma", dist.Uniform(0, 1e-3)).unsqueeze(-1)
    w = pyro.sample("w", dist.Normal(0, 1).expand(data.shape).to_event(1))
    threshold = torch.min(torch.topk(w, int(data.shape[0]*0.1)).values)
    w_new = torch.nn.functional.relu(w-threshold)
    x_t = pyro.deterministic("x_t", x_0 + sigma * w_new.cumsum(dim=-1))

    sigma_z = pyro.sample("sigma_z", dist.Uniform(0, 1e-3)).unsqueeze(-1)
    z_t = pyro.sample("z_t", dist.Normal(x_t, sigma_z).expand(data.shape).to_event(1), obs=data)

Data

df = pd.read_csv(
    'https://s3.eu-central-1.amazonaws.com/mira.collector/data.csv',
    index_col=0)
r = torch.tensor(df.price)

Training

pyro.clear_param_store()
pyro.set_rng_seed(1234567890)
num_steps = 1001
optim = ClippedAdam({"lr": 0.05, "betas": (0.9, 0.99), "lrd": 0.1 ** (1 / num_steps)})
guide = AutoDiagonalNormal(model)
svi = SVI(model, guide, optim, Trace_ELBO())
losses = []

for step in range(num_steps):
    loss = svi.step(r) 
    losses.append(loss)
    if step % 50 == 0:
        median = guide.median()
        print("step {} loss = {:0.6g}".format(step, loss))
pyplot.figure(figsize=(9, 3))
pyplot.plot(losses)
pyplot.ylabel("loss")
pyplot.xlabel("SVI step")
pyplot.xlim(0, len(losses))
pyplot.ylim(min(losses), 20)

Smoothing

# We will pull out median log returns using the autoguide's .median() and poutines.
with torch.no_grad():
    pred = Predictive(model, guide=guide, num_samples=100, parallel=False)(r)
x_t = torch.mean(pred['x_t'],axis=0)
df_pred =  pd.DataFrame(x_t.numpy().squeeze(),df.index,columns=['x_t'])

pd.concat([df.price, df_pred.x_t], axis=1).plot()
1 Like