Hello, I am implementing a standard and simple dynamical state space model of the form
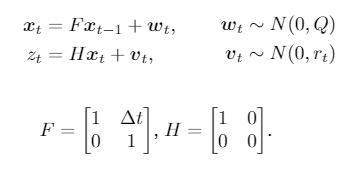
where my state x_t contains the position variable x and its velocity variable v of an unknown object. We only observe the position variable x of the object and this observation is denoted by z_t. I want to capture this behaviour in the model and infer latent variables x_t using the SVI method.
There is one twist. During some time interval, the measurements are unavailable. My goal is that the inference procedure is still able to infer these unobserved states using the model structure. (This occluded interval does not have to be at the end, so I am not interested in forecasting).
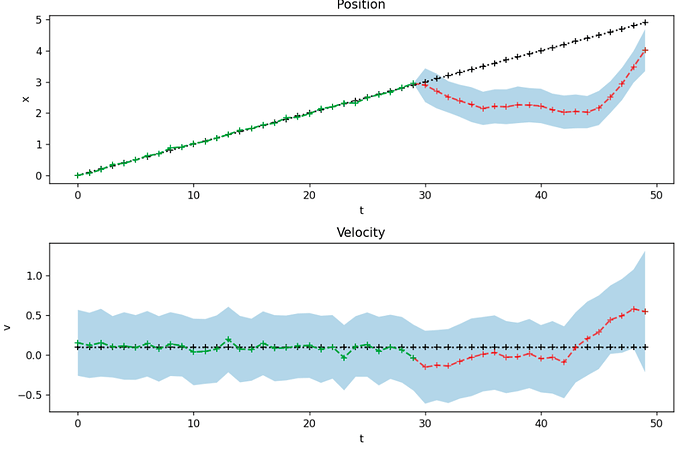
I created the following implementation for 50 time steps , where one time step is of size 1. There are no measurements from time step 30 up until 50. So the last 20 time steps.
# Model
def model(prior, F, Q, r, data):
P0 = torch.eye(prior.shape[0])
prev_state = pyro.sample("prior", dist.MultivariateNormal(prior, P0))
for t in pyro.markov(range(0,len(data))):
# Transition model formula
state = pyro.sample("state_{}".format(t), dist.MultivariateNormal(prev_state, Q))
# Nonlinearity function h(x_t)
c_state = state[0]
# Occlusion
r_t = r
if t >= occ_start and t<=occ_start+occ_dur:
r_t=10000000000.
# Observation model formula
pyro.sample("measurement_{}".format(t), dist.Normal(c_state, r_t), obs = data[t])
prev_state = F@state.T
I implemented two separate mean field guides that behave similarly. The first one considers 50 separate latent states and their 50 corresponding covariance matrices.
The second one combines these 50 states into one large state latent mean and one big corresponding covariance matrix.
# Guide 1
def guide(prior, F, Q, r, data):
P0 = torch.eye(prior.shape[0])
prev_state = pyro.sample("prior", dist.MultivariateNormal(prior, P0))
# prev_state = torch.tensor([0.1,0.1])
for t in pyro.markov(range(0,len(data))):
# Mean and covariance parameters
x_value = pyro.param("x_value_{}".format(t), torch.zeros(prior.shape[0]))
var_value = pyro.param("var_value_{}".format(t), P0,
constraint=dist.constraints.lower_cholesky)
# x_t = N(x_value, var_value)
state = pyro.sample("state_{}".format(t), dist.MultivariateNormal(x_value, scale_tril=var_value))
And the second guide:
# Guide, with big combined multivariate distribution
def guide(prior, F, Q, r, data):
P0 = torch.eye(prior.shape[0])
n = prior.shape[0] # Equal to 2
prev_state = pyro.sample("prior", dist.MultivariateNormal(prior, P0))
loc = pyro.param("loc", Variable(2.0*torch.ones(prior.shape[0]*data.shape[0]), requires_grad=True))
scale = pyro.param("scale_tril", Variable(5.0*torch.eye(prior.shape[0]*data.shape[0]), requires_grad=True),
constraint=dist.constraints.lower_cholesky)
for t in pyro.markov(range(0,len(data))):
# Mean and covariance parameters
x_value = loc[t*n:t*n+n]
var_value = scale[t*n: t*n + n, t*n: t*n + n]
# x_t = N(x_value, var_value)
state = pyro.sample("state_{}".format(t), dist.MultivariateNormal(x_value, scale_tril=var_value))
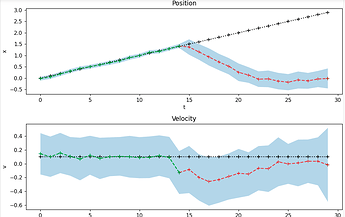
These both give similar results like this
The problem here is that the estimates of the confidence bounds do not behave as expected. When you do not get new measurements anymore, you would expect that the inference procedure becomes more uncertain about its prediction every time step. Therefore I would expect the uncertainty and therefore the confidence bounds to grow if you receive no measurements at the end.
This is not the case. How can I fix this?
I was thinking about using a structured guide, but a proper mean field guide should still be able to incorporate the time dependencies of the states at different time steps.
Side note: I implemented this occlusion of measurements by drastically increasing the variance of the measurement during this interval. I specifically did not use obs_mask since, if I increase this to more dimensions and to a non-linear variant I do not want my entire measurement to be unobserved but only part of it.