I know that SVI with subsampling can handle large dataset. Now I’m trying to use HMCECS on a large dataset (I have already run my HMCECS model on a subsampled dataset). Is this algorithm same as SVI with subsampling that has can handle the large dataset?
You can follow the references for the scalability. IIRC there is OOM issue with very large dataset.
Thanks for your reply! My dataset is not particularly large, and now the HMCECS algorithm has already worked on it. BTW can you briefly explain the difference between HMCECS and classic HMC in terms of the performance, accuracy etc. ? if it’s convenient for you. I really appreciate it!
Hi @zephyrus,
Those are some big questions. The algorithm is detailed in Hamiltonian Monte Carlo with Energy Conserving Subsampling. At its core, it uses a likelihood estimator to evaluate instead of the full likelihood to make the gradient cost constant with respect to data size. HMC evaluates the gradient often to produce new proposals that are probable. This makes HMC expensive for datasets with many data points because the gradient computation is linear in the number of data points.
As far as I’m aware, there are no systematic studies of the performance of HMCECS, both in terms of (asymptotic) convergence guarantees (like with have for HMC) or performance in terms of accuracy (beyond what’s in the referenced paper). I have not had much time to play with the implementation, so I can’t give you anecdotal advice.
Please ping me with your use case. I’d be interested to know.
Best, Ola
Hi @OlaRonning ,
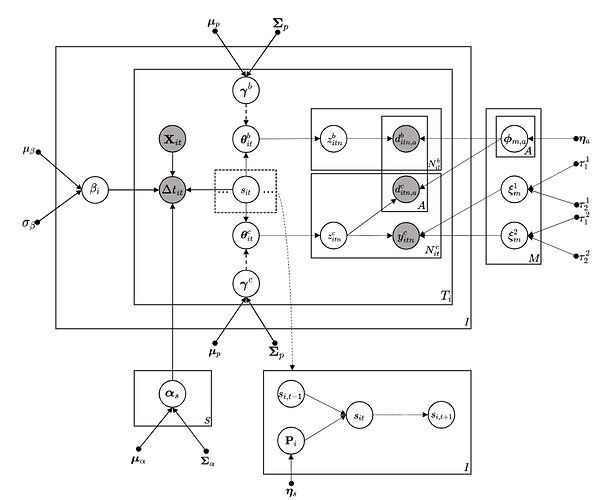
Thanks for your detailed reply! My model is a complex probabilistic model that combines HMM with a topic model. What I want to do is modeling users’ different preferences under different activity hidden states and get some insights. The concrete data is users’ history behaviors, which is a quite large dataset when the number of users is large. Therefore I consider to using HMCECS. However, from the perspective of the result that I just got yesterday, the HMCECS seemed to perform poorly on a subsampled 1000 users dataset (the n_eff is very low and the parameters are not converged). Further more, It took me almost 3 days to run this model on a 2080Ti GPU, which is really slow I think. Now I have to switching to classic mean-field approximation variational inference with analytical parameter updating formulas(Really feel upset because of the complex derivation work 
). Here is the DAG representation of my model. I really appreciate it if you can provide me with some advice about model, optimization algorithm etc. BTW, I did not use the Taylor proxy in HMCECS.
@OlaRonning If you are interested in my model code. You can join the collaborators, and I have invited you to my private repository. My GitHub name is the hjnnjh 
That is an elaborate DAG c: and thanks for the invite. I won’t have time to review the model code thoroughly, but I can give it a quick scan.
Some general observations, reducing max_tree_depth will positively affect runtime (at the cost of more autocorrelation). If your step_size is tiny and you hit max_tree_depth, you are probably getting highly correlated samples (and therefore poor \hat{R} and ESS). Check the acceptance rate of the Gibbs sampler; if it’s low, your subsample is rarely updated. In general, I would expect HMCECS to require more samples than HMC (however, I reiterate I haven’t played much with the implementation).
As an alternative (before you derive MF-VI by hand) you could try SVI with TraceGraph_ELBO.
Best, Ola
Thanks for your advice. I really appreciate it. In my model, I have several high-dimensional Dirichlet distributions (approximately 4000-5000), and I have already tried SVI with TraceEnum_ELBO in Pyro. However, some autoguides like AutoNormal or AutoLowRankMultivariateNormal cannot handle these high-dimensional Dirichlet distributions effectively. Additionally, I have noticed that some optimized parameters tend to converge around their initial values, which has led me to question the suitability of the Probabilistic Programming Language (PPL) in my model. Nevertheless, I haven’t yet tried using SVI with TraceGraph_ELBO in Numpyro. I plan to give it a try after getting some rest, as it’s currently almost 1:00 a.m. here in China.
With a Gaussian guide and a Dirichlet distribution, you’ll use the stick breaker transforms. With 4000-5000 dimensions, the values will be pretty small (especially if guide_loc >> 0). Consider using float64 instead (see example below).
x = Normal(4, 1).sample(PRNGKey(0), (5000,))
print((StickBreakingTransform()(x) == 0.0).sum()) # 1905
from jax.config import config;
config.update("jax_enable_x64", True)
x = Normal(4, 1).sample(PRNGKey(0), (5000,))
print((StickBreakingTransform()(x) == 0.0).sum()) # 0
@OlaRonning Looks great! However, there is still an issue: switching to float64 actually consumes more GPU memory (It might differ in jax , but it’s something important to consider in torch ). Nonetheless, I appreciate your advice. I’m now going to explore using TraceGraph_ELBO in Numpyro .
You are right; double precision will be slower, no matter the language. But consider that if your data structure can’t represent what you are modeling, it doesn’t matter how efficient it is.
@OlaRonning Really incredible after switching to SVI with TraceGraph_ELBO! It’s very fast (I spent less than 1 minute running on a sub-dataset) and the final loss is really low. I’ll check the optimized parameters later.
I still remember I have tried TraceEnum_ELBO in Pyro, which performs bad on my model (The speed is a little bit slow and the final loss is very large with high variance).