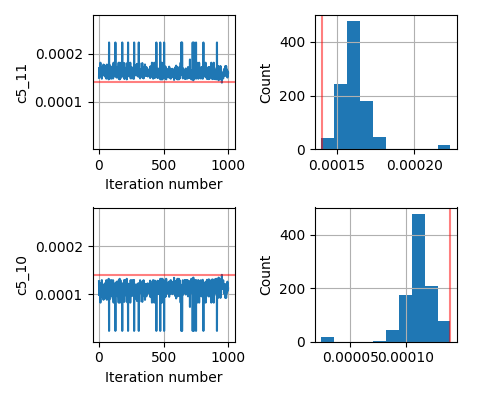
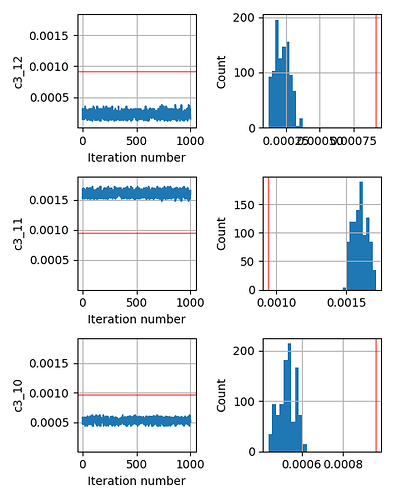
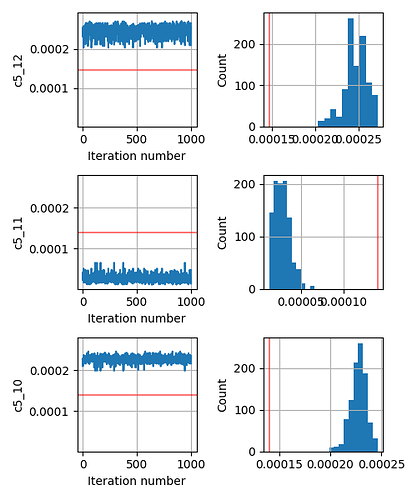
I am working on a possibly high dimensional problem (somewhere between 45-60 parameters). Since the forward problem is expensive (involves eigenvalue problem) we are using relatively faster kernels like SA instead of NUTS.
- We first set up a synthetic data from the forward problem that we have, so that there is no noise and we can test if the SA kernel works perfectly. This did not work when we threw the entire set of parameters at the code.
- Then we reduced the number of parameters to 2 (holding all the others fixed to their “true” value as used in generating the synthetic data). Doing this, the default SA failed to converge again.
- Next we changed the
adapt_state_sizeto 100 in theSAkernel. This successfully returns the 2 parameters from the simulation. - We then started slowly increasing the number of parameters to 4. But this failed again. Even with
adapt_state_size = 100.
The current model we are testing with is exceptionally simple (does not involve an eigenvalue problem):
def model():
# sampling from a uniform prior
c0 = numpyro.sample(f'c0', dist.Uniform(cmin[0], cmax[0]))
c1 = numpyro.sample(f'c1', dist.Uniform(cmin[1], cmax[1]))
c2 = numpyro.sample(f'c2', dist.Uniform(cmin[2], cmax[2]))
c3 = numpyro.sample(f'c3', dist.Uniform(cmin[3], cmax[3]))
# the forward problem
pred = fixed_part + param_coeff[0] * c0\
+ param_coeff[1] * c1\
+ param_coeff[2] * c2\
+ param_coeff[2] * c3
pred = pred - data
return numpyro.factor('obs',
dist.Normal(pred, jnp.ones_like(pred)).\
log_prob(jnp.zeros_like(data)))
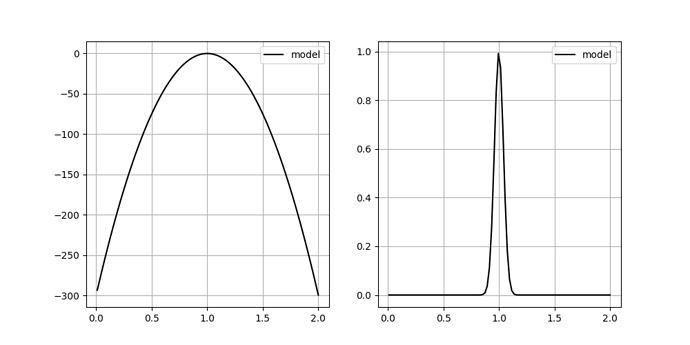
As an added info, the terrain of our minimizing function (or likelihood function) for different values of any such parameter c looks like a very sharp gaussian.
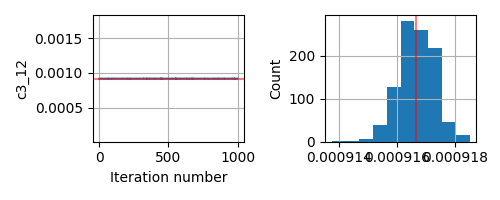
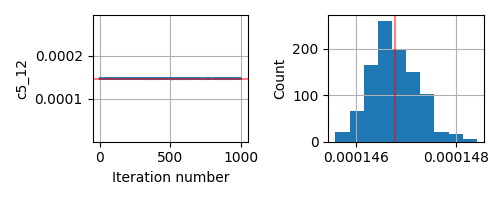
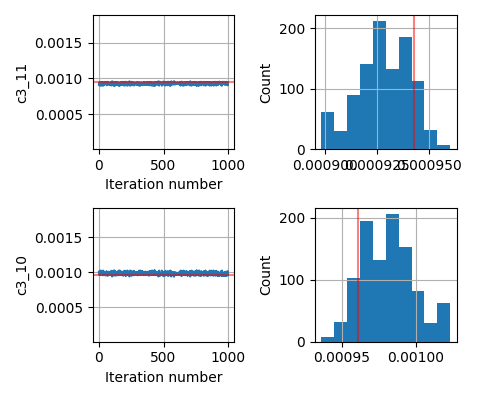
This seems to be a relatively simple problem that SA should be able to handle. But even if I change the prior from Uniform to Normal centered around the true parameter, the inversion does not give me the correct answer.
What am I doing wrong? Should I rescale my parameter values? They are of the magnitudes of the order 1e-2 and 1e-3. Should I change the kernel? Should I add some other key in the kernel or the MCMC function call?