Hello,
I would like to use something similar to what is proposed in the deep Markov model but I am gonna use longer sequences than those in the tutorial. I would like to know if there is a way of implementing truncated backprop for the rnn in the model and if there are any resources that explain how to do so.
Thank you,
NB
can you please provide more details?
note that the rnn in pyro’s dmm is only in the guide and not in the model. note in addition that the rnn consumes the observations and as such it doesn’t directly interact with the (stochastic) latent variables. note also that pyro doesn’t do any “deep learning magic”, i.e. all the deep learning happens directly in user code. so the rnn in the guide is entirely controlled by the user. any deep learning tricks the user may want to apply (unless it’s something more exotic like some sort of gradient surgery) can be done directly to the rnn just as in vanilla pytorch. so the upshot is if you want to do truncated backprop on a pytorch rnn you’re really asking a deep learning question and the right place to look for resources is probably elsewhere.
finally, i would add that if you want do something like the deep markov model on long sequences i would suggest you use a mean field guide otherwise it will be quite slow to train.
Thank you!
My ultimate goal is to implement the switching linear dynamical system model that is in this paper: https://arxiv.org/pdf/1603.06277.pdf to analyze some video data. The paper however uses an inference procedure that seems to be largely incompatible with pyro but I was hoping that just doing variational inference would work. However, I haven’t worked with temporal data before so I was using the tutorials as examples.
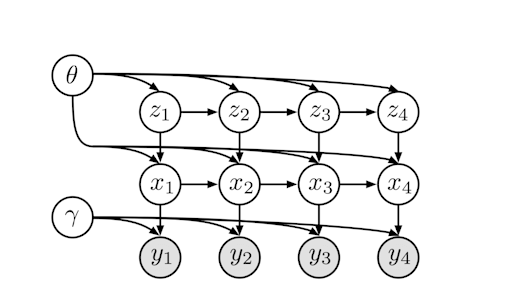
The model looks like this
where z_n is a discrete markov chain and to get the y_i we use a nerual network just like with a VAE. My original idea was to first do the model side enumeration to marginalize out the z_i and then use a meanfield family for the x_i,A,B random variables (using a vanilla neural network for p(x_i|y_i)$ probabilities in the guide. Finally, I could use the infer_discrete function to the inference on the z_i. However, reading the dmm tutorial it seemed like it would make sense to use an rnn to properly condition on more than just the immediate “y_i” so that’s why I was asking.
I was a bit confused about the truncated backprop because as far as I remember when you are calling the rnn you detach the hidden state at some point backpropagate , detach, continue calling the rnn, backpropagate, and so on. But with pyro, at least as I understand it, when you call svi step it does the backpropagation through the network for us and I was unsure about how to control it in this way.
I am sorry if there is anything that is wrong here. I haven’t worked with temporal data before so that is why I am a bit confused.
If I do manage to successfully train the model I would be more than happy to turn it into a tutorial if someone finds it useful.
Thank you again.
discrete latent variables in this kind of setting present a real challenge. e.g. if you try to marginalize them out you’ll generally get a cost that’s exponential in the length of the time series. if you can i’d avoid discrete latent variables. if they are necessary to your use case you probably need to think carefully about appropriate custom inference strategies that can accommodate the discrete structure.
Why is there an exponential cost in this case and not in the regular HMM examples in the tutorials? Or is there also an exponential cost in both situations?(edit: nvm I see now where the exponential cost comes from. I’ll try to reformulate it to get rid of the discrete states. Thank you, this saved me a lot of time)
incidentally i was playing around with a mean field variant of the dmm here. from what i recall this was ~5x faster to train.
1 Like
Thank you!
I’ll take a look.