I’m developing a probabilistic error model in Pyro, where I’m modeling errors as samples from a transformed Gamma distribution. My goal is to use MCMC to simulate realistic error values based on this model. I’ve already created a toy dataset of errors sampled from a known Gamma distribution. However, I’ve encountered numerical instability issues during optimization, specifically with the Gamma distribution’s location parameter becoming NaN. How can I address these instability problems and successfully implement MCMC for error simulation in my Pyro model?
import pandas as pd
import torch
from torch import nn
from torch.distributions.normal import Normal
from torch.distributions.log_normal import LogNormal
from torch.distributions.gamma import Gamma
from torch.distributions.transforms import AffineTransform
from torch.distributions import constraints
from torch.utils.data import DataLoader, TensorDataset
import numpy as np
import pyro
from pyro.optim import Adam
from pyro.infer import SVI, Trace_ELBO
import pyro.distributions as dist
n = 1000
loc = torch.tensor(2.)
scale = torch.tensor(2.)
x_shift = torch.tensor(1)
errors = (-1)*Gamma(loc, scale).sample((n,)) + x_location
The data looks:
And the histogram:
Then I build two models, the error model and the data generator:
def error_model_gamma(errors):
loc = pyro.param("loc_dist", torch.tensor(2.))
scale = pyro.param("scale_dist", torch.tensor(2.))
x_shift = pyro.param("x_shift",torch.tensor(1.))
with pyro.plate("errors", errors.shape[0]) as error_it:
error = pyro.sample(f"error_{error_it}",
dist.TransformedDistribution(dist.Gamma(loc, scale),
AffineTransform(loc=x_shift, scale=torch.tensor(-1))),
obs=errors[error_it])
return error
#
def data_model_gamma(y):
"""Data model to sample from."""
loc = pyro.param("loc_dist")
scale = pyro.param("scale_dist")
x_shift = pyro.param("x_shift")
with pyro.plate("preds", y.shape[0]):
return pyro.sample("pred",
dist.TransformedDistribution(dist.Gamma(loc, scale),
[AffineTransform(loc=x_shift + y, scale=torch.tensor(-1))])
)
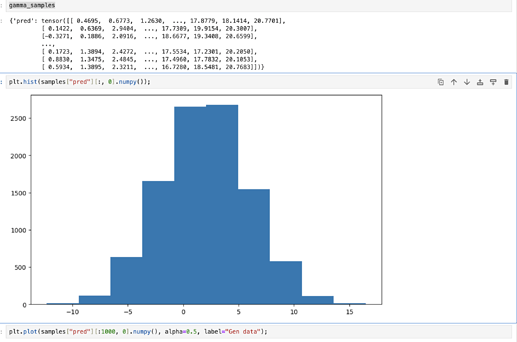
Even if I put the same values (loc, scale, x_shift) as during the data generation: the MC stage does not produce the same output:
nuts_kernel_gamma = pyro.infer.mcmc.NUTS(data_model_gamma)
mcmc_log_gamma = pyro.infer.mcmc.api.MCMC(nuts_kernel_gamma, num_samples=1000, warmup_steps=100)
mcmc_log_gamma.run(torch.range(0,20))
Is there something wrong with my models?
A follow-up quesiton. When I change the parameters values and try to train them:
def guide_error_gamma(errors):
# Guide parameters for the Gamma distribution
guide_loc = pyro.param("guide_loc", torch.abs(torch.mean(errors)), constraint=dist.constraints.positive)
guide_scale = pyro.param("guide_scale", torch.std(errors), constraint=dist.constraints.positive)
guide_x_shift = pyro.param("guide_x_shift", torch.max(errors))
with pyro.plate("errors", errors.shape[0]) as error_it:
pyro.sample(f"error_{error_it}",
dist.TransformedDistribution(dist.Gamma(guide_loc, guide_scale),
AffineTransform(loc=guide_x_shift, scale=torch.tensor(-1))))
# Set up the optimizer
optimizer = Adam({"lr": 0.00001})
# Set up the inference algorithm
svi = SVI(error_model_gamma, guide_error_gamma, optimizer, loss=Trace_ELBO())
# Run the optimization
num_iterations = 20000
for iteration in range(num_iterations):
loss = svi.step(errors)
if iteration % 1 == 0:
print(f"iteration {iteration} Loss: {loss}")
print(pyro.param("loc_dist"), pyro.param("scale_dist"), pyro.param("x_shift"))
The loc_dist after just one iteration is set to nan. Any idea how to debug and solve this?
I create a similar experiment using Normal distribution and without AffineTransform . It works perfectly fine.