Regression with exponential errors

Misc.
1

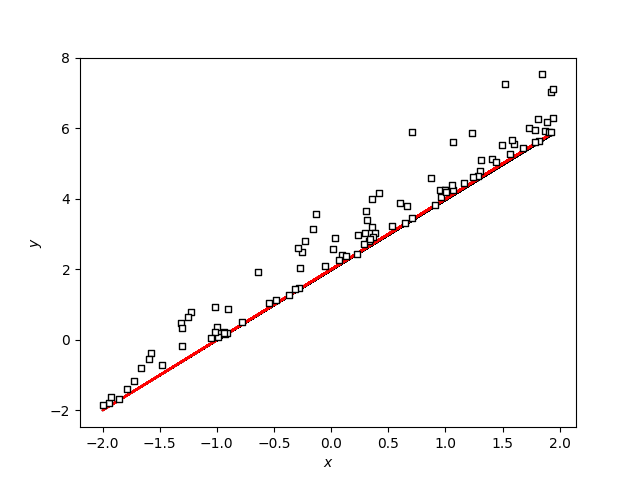
I am trying to create regression with exponential distributed errors.

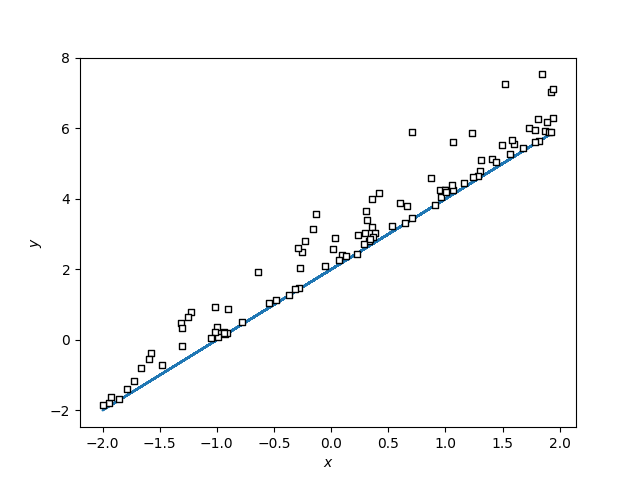
Figure_1

I am trying to estimate the regression like this

import numpy as np
import numpyro
from numpyro import distributions as dist
from numpyro.infer import MCMC, NUTS


import jax
import jax.numpy as jnp

numpyro.set_host_device_count(2)
import matplotlib.pyplot as plt

a = 2
b = 2
lam = 1/2
x_data = np.random.uniform(-2, 2, 100)
y_data = a + b * x_data + np.random.exponential(lam, x_data.size)

def model1(x=None, y=None):
    a = numpyro.sample("a", dist.Uniform(1.0, 3.0))
    lam = numpyro.sample("lambda", dist.Exponential(1))

    M = 0.0
    if x is not None:
        bM = numpyro.sample("b", dist.Uniform(0.0, 4.0))
        M = bM * x

    mu = numpyro.deterministic("mu", a + M, )


    ExponentialShift = dist.TransformedDistribution(
        dist.Exponential(rate=lam),
        dist.transforms.AffineTransform(mu, 1),
    )
    with numpyro.plate("data", len(x)):
        numpyro.sample("obs", ExponentialShift, obs=y)


# Using the model above, we can now sample from the posterior distribution using the No
# U-Turn Sampler (NUTS).
sampler1 = MCMC(
    NUTS(model1),
    num_warmup=3000,
    num_samples=10000,
    num_chains=2,
    progress_bar=True,
)
sampler1.run(jax.random.PRNGKey(0), x_data, y=y_data)


summary = sampler1.get_samples()

a_hat = summary["a"].mean()
b_hat =  summary["b"].mean()


plt.scatter(x_data, y_data, marker="s", s=22, c="w", edgecolor="k", zorder=1000)
plt.plot(x_data, (a_hat + b_hat * x_data), color="k", lw=1.5)
plt.plot(x_data, a + b * x_data, color = "r")
plt.xlabel("$x$")
plt.ylabel("$y$")
plt.show()

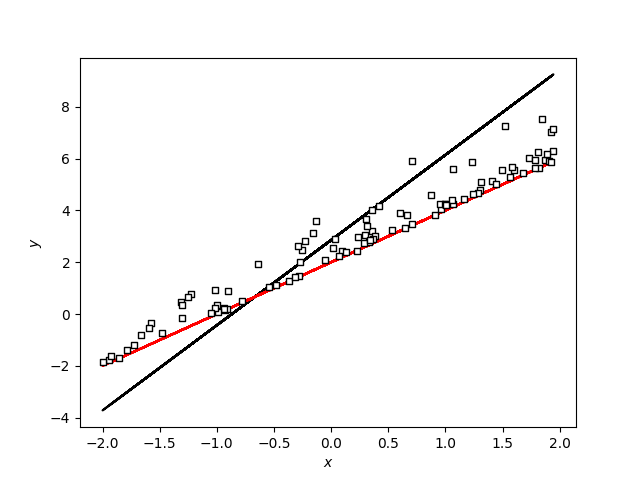
Figure_2

I think the problem is that I am applying the AffineTransform incorrectly since when I modify my example like that it seems to work


def model2(x, y):
    a = numpyro.sample('a', dist.Normal(0, 10))
    b = numpyro.sample('b', dist.Normal(0, 10))
    lambda_err = numpyro.sample('lambda', dist.Exponential(1.0))
    
    mean = a + b * x
    err = numpyro.sample('err', dist.Exponential(lambda_err), sample_shape=(len(x),))
    numpyro.sample('y', dist.Normal(mean + err, .001), obs=y)


# Using the model above, we can now sample from the posterior distribution using the No
# U-Turn Sampler (NUTS).
sampler2 = MCMC(
    NUTS(model2),
    num_warmup=3000,
    num_samples=10000,
    num_chains=2,
    progress_bar=True,
)
sampler2.run(jax.random.PRNGKey(0), x_data, y=y_data)


summary = sampler2.get_samples()

a_hat = summary["a"].mean()
b_hat =  summary["b"].mean()


plt.scatter(x_data, y_data, marker="s", s=22, c="w", edgecolor="k", zorder=1000)
plt.plot(x_data, (a_hat + b_hat * x_data), color="k", lw=1.5)
plt.plot(x_data, a + b * x_data, color = "r")
plt.xlabel("$x$")
plt.ylabel("$y$")
plt.show()

Figure_3

2

exponentially distributed how? are you saying the error is always positive and never negative? in your first figure it looks like your noise is heteroscedastic and increases in magnitude from left to right

3

Yes the error terms would be always positive. So the generating process looks like this:

y= a+b*x+e e~exp(lambda)

And in this way I also generated the data for the picture. It’s in the first part of the code how I generated the data.
That the errors look heteroskedastic is a unfortunate coincidence.

4

presumably you want something like

def model2(x, y):
    a = numpyro.sample('a', dist.Normal(0, 10))
    b = numpyro.sample('b', dist.Normal(0, 10))
    lambda_err = numpyro.sample('lambda', dist.Exponential(1.0))
    
    mean = a + b * x
    numpyro.sample('y', dist.Exponential(mean, lambda_err), obs=y)

the problem with this is that it strictly requires that y is larger than mean everywhere so your model2 with

numpyro.sample('y', dist.Normal(mean + err, .001), obs=y)

may perform better