Rasch model

Misc.
1

Hi!

I’m trying to implement a vectorized Rasch model (for reference: Rasch model).

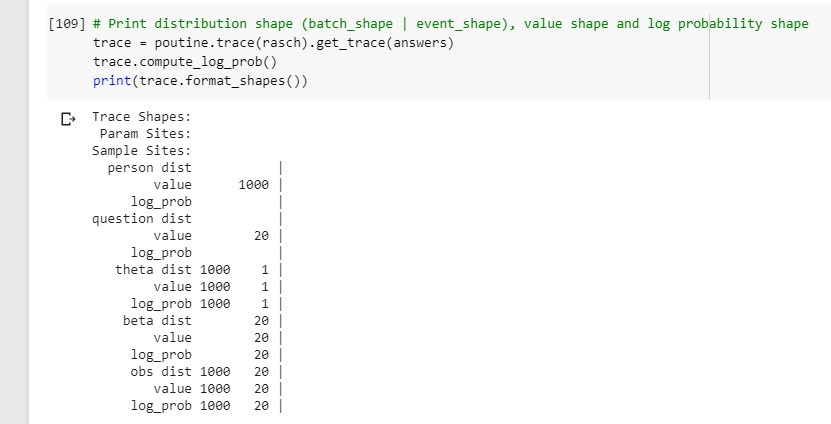
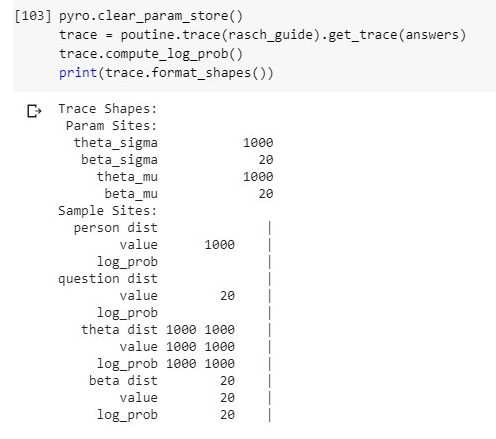
I get the SVI to function, but achieve no convergence with SGD on the guide specified below. With Adam I achieve convergence but low such. With AutoGuide, SGD convergence is better but precision is still bad. Any suggestions on whether the issue lies with my model or my guide?

Generate data:

n_persons = 1000
n_questions = 20

np.random.seed(543678)
true_theta = np.random.normal(loc=0, scale=1, size=(n_persons,1))
true_theta = np.tile(true_theta, n_questions)
true_beta = np.random.normal(loc=0, scale=1, size=(1,n_questions))

likelihood = np.exp(true_theta - true_beta) / (1 + np.exp(true_theta - true_beta))

answers = np.random.binomial(size=(n_persons, n_questions), p=likelihood, n=1) # calculate answers based on theta and likelihood function
answers = torch.tensor(answers).float() # convert to tensor

Define model:

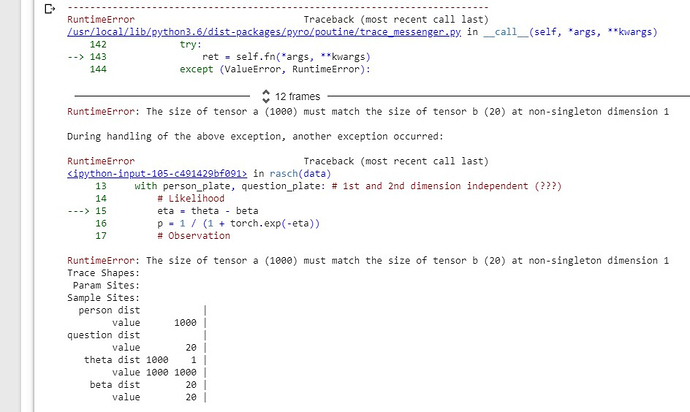
def rasch(data):
    n_persons = data.shape[0]
    n_questions = data.shape[1]
    person_plate = pyro.plate('person', n_persons, dim=-2)
    question_plate = pyro.plate('question', n_questions, dim=-1)

    with person_plate:
        theta = pyro.sample('theta', pyro.distributions.Normal(0, 1))
        assert theta.shape == (n_persons, 1)
    with question_plate:
        beta = pyro.sample('beta', pyro.distributions.Normal(0, 1))
        assert beta.shape == (n_questions,)
    with person_plate, question_plate:
        # Likelihood
        eta = theta - beta
        p = 1 / (1 + torch.exp(-eta))
        # Observation
        obs = pyro.sample('obs', dist.Bernoulli(p), obs=data)
        assert obs.shape == (n_persons, n_questions)
    return obs, theta, beta

Define guide:

def rasch_guide(data):
    n_persons = torch.tensor(data.shape[0])
    n_questions = torch.tensor(data.shape[1])
    person_plate = pyro.plate('person', n_persons, dim=-2)
    question_plate = pyro.plate('question', n_questions, dim=-1)
    
    with person_plate:
        theta_mu = pyro.param('theta_mu', torch.tensor(0.))
        theta_sigma = pyro.param('theta_sigma', torch.tensor(1.), constraint=constraints.positive)
        theta = pyro.sample('theta', pyro.distributions.Normal(loc=theta_mu, scale=theta_sigma))
    with question_plate:
        beta_mu = pyro.param('beta_mu', torch.tensor(0.))
        beta_sigma = pyro.param('beta_sigma', torch.tensor(1.), constraint=constraints.positive)
        beta = pyro.sample('beta', pyro.distributions.Normal(beta_mu, beta_sigma))
    return {'theta': theta, 'beta': beta}

I also have questions regarding on how to build a model for many posterior parameters, as in this case. I need to be able to extract the posterior beta_mu and beta_sigma, which are as many as there are questions. The only approach I’ve found is sampling from the approximated posterior distribution using the parameterized guide, like so:

posterior_distribution = rasch_guide(answers)
theta_posterior = posterior_distribution['theta']
beta_posterior = posterior_distribution['beta']
print(theta_posterior.shape)
print(beta_posterior.shape)

However, I’m not sure this is a valid approach at all, as the values I obtain have low correlations with the prior data (true values).

2

if i understand your model correctly i think you may need to initialize your parameters in the guide with vector and not scalar tensors, e.g.

theta_mu = pyro.param('theta_mu', torch.zeros(n_persons))

3

Thanks for answering!

I just tried that, however, I’m getting problems with the tensor broadcasting when calculating eta:

image
image.jpg944×564 126 KB

These are the tensor shapes for the model:

image
image.jpg831×424 50 KB

And for the guide:

image

4

it’s a bit difficult for me to see what might be wrong without running the code. can you please provide a complete executable script, i.e. one with import statements at the top, an SVI instance, etc.?

5

Here is the full notebook, if you want to have a look:

6

great, thanks. i think you may just need to make the following change in the guide:

theta = pyro.sample('theta', pyro.distributions.Normal(theta_mu.unsqueeze(-1), theta_sigma.unsqueeze(-1)))

1 Like
7

This was very helpful, many thanks!