Hello. I’m interested in using the SVI model+guide approach to model a normal distribution given some priors (in this case a normal distribution of mean 5 and stdev 5) and some observations (in this case the values 10 and 90).
This is how my prior’s PDF looks like:
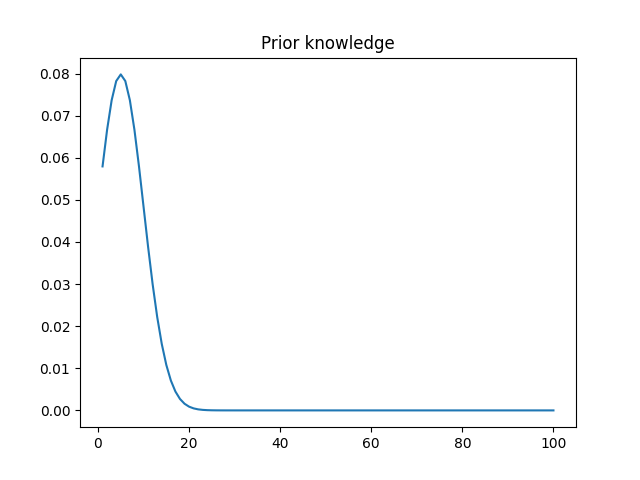
And this is the PDF learned by my code (mean 49.3, stdev 0.79):
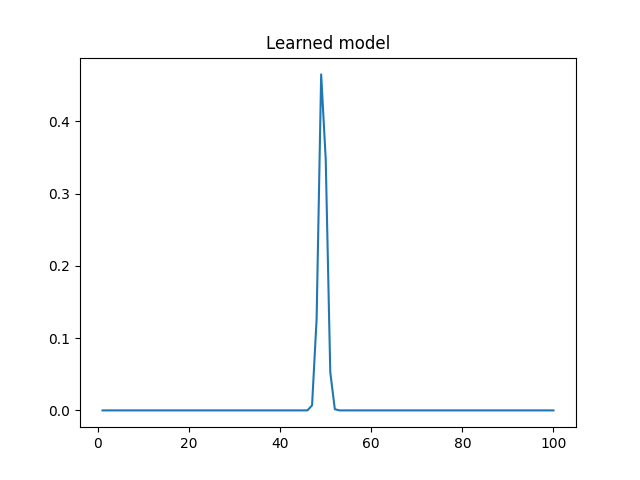
My questions are:
- Why don’t I get a larger stdev? That really doesn’t look like a distribution that generated 10 and 90
- How can I learn a model that is based on both the priors and the observations? My reasoning is that I expect the prior distribution to have significant value, but I’d like to shift it towards the observations. Similarly to a coin that I expect to be fair, but that might be biased. If I get three tails, I’m not gonna say it’s biased, but if I get 10 more tails, then it’s probably biased.
This is my code:
import matplotlib.pyplot as plt
import numpy as np
import pyro
from pyro.distributions import LogNormal, Normal
from pyro.infer import SVI, Trace_ELBO
import torch
from torch.distributions import constraints
pyro.enable_validation(True)
pyro.clear_param_store()
pyro.set_rng_seed(42)
data = torch.tensor([10, 90])
def model(data):
mean = torch.tensor(5.0)
stdev = torch.tensor(5.0)
payday = pyro.sample('m0', Normal(mean, stdev))
with pyro.iarange('data_loop', len(data)):
pyro.sample('m0_decoy', Normal(payday, 0.001), obs=data)
def guide(data):
mean = pyro.param('mean', torch.tensor(5.0))
stdev = pyro.param('stdev', torch.tensor(5.0), \
constraint=constraints.positive)
pyro.sample('m0', Normal(mean, stdev))
def plot(data, mean, stdev):
fig = plt.figure()
x_range = torch.tensor(np.linspace(1, 100, num=100))
y = np.exp(Normal(mean.data, stdev.data).log_prob(x_range))
plt.title('Learned model')
plt.plot(x_range, y)
plt.show()
optim = pyro.optim.Adam({'lr': 0.1})
elbo = Trace_ELBO()
svi = SVI(model, guide, optim, loss=elbo)
for i in range(1001):
svi.step(data)
if i % 50 == 0:
mean = pyro.param('mean')
stdev = pyro.param('stdev')
print("mean: {}".format(mean))
print("stdev: {}".format(stdev))
pdf = plot(data, mean, stdev)