Question regarding Gaussian mixture model (GMM) using EM algorithm

Tutorials
1

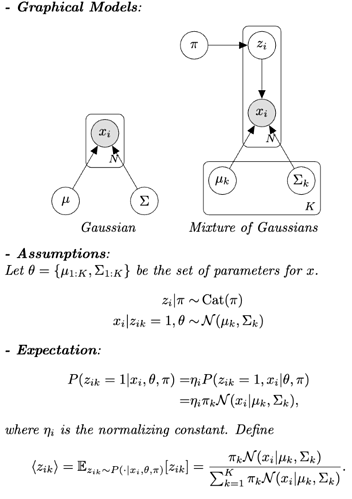
Hello everyone! I have read the GMM tutorial on the website, and I wanted to create a naive version of GMM where the mixture weights, means, covariance matrices are treated as learnable parameters instead of latent variables; in other words, no prior distributions are assumed for them. The model assumptions and the E-step are shown in the picture attached.

GMM
GMM610×866 46.3 KB

I think the major problem I had was I don’t know how to use the same set of parameters for model and guide. In pyro, it seems that the parameters (theta) for the generative process is defined in a model, while the parameters (phi) for the inference process is defined in a guide. In EM algorithm, we essentially use the same set of parameters for the E-step and M-step, and I don’t know how to reflect this in my code.

Here’s my model and guide:

def model(data, K=3): 
    num_obs,num_dim = data.shape

    with pyro.plate("data", size=num_obs):
        assignment = pyro.sample("assignment", dist.Categorical(torch.ones(K)/K))  
        means = torch.zeros(K, num_dim)
        scale_tril = torch.eye(num_dim).repeat(K, 1, 1)  
        pyro.sample("obs", dist.MultivariateNormal(means[assignment], scale_tril=scale_tril[assignment]), obs=data)

def guide(data, K=3):
    num_obs,num_dim = data.shape

    # define learnable parameters: mixture weights, means, covariance matrices
    weights = pyro.param("weights", torch.ones(K)/K, constraint=dist.constraints.simplex)
    means = pyro.param("means", torch.randn(K, num_dim))  
    chol_factor = pyro.param("chol_factor", torch.eye(num_dim).repeat(K, 1, 1))
    scale_diag = pyro.param("scale_diag", torch.ones(K, num_dim), constraint=dist.constraints.positive)
    scale_tril = chol_factor @ torch.diag_embed(scale_diag)   

    with pyro.plate("data", size=num_obs):
        # log(pi_k) + log(Normal(x_i | mu_k, Sigma_k))
        log_probs = torch.stack([dist.MultivariateNormal(means[k], scale_tril=scale_tril[k]).log_prob(data) for k in range(K)], dim=-1) + torch.log(weights)  
        assignment_probs = torch.exp(log_probs - torch.logsumexp(log_probs, dim=1, keepdim=True))
        assignment = pyro.sample("assignment", dist.Categorical(probs=assignment_probs))

Here is how I generate my data:

weights = np.array([2/8, 5/8, 1/8])
means = np.array([[1, 2], 
                  [5, 6],
                  [3, 1]])
covariances = np.array([[[1.0, 0.2], [0.2, 1.5]],
                        [[3, -0.3], [-2, 9]],
                        [[1.2, 0.4], [0.4, 1.3]]])
def sample_from_mixture(weights, means, covariances, num_samples=100):
    num_components = len(weights)
    components = np.random.choice(num_components, size=num_samples, p=weights)
    samples = np.array([
        np.random.multivariate_normal(means[comp], covariances[comp])
        for comp in components
    ])
    return samples

num_samples = 1000
samples = sample_from_mixture(weights, means, covariances, num_samples)
samples = torch.tensor(samples, dtype=torch.float)

Here’s my training setup:

pyro.clear_param_store()
optim = Adam({"lr": 0.001, "betas": [0.8, 0.99]})
elbo = Trace_ELBO()
svi = SVI(model, guide, optim, elbo)

num_steps = 20000
for step in range(num_steps):
    loss = svi.step(samples, K=3)

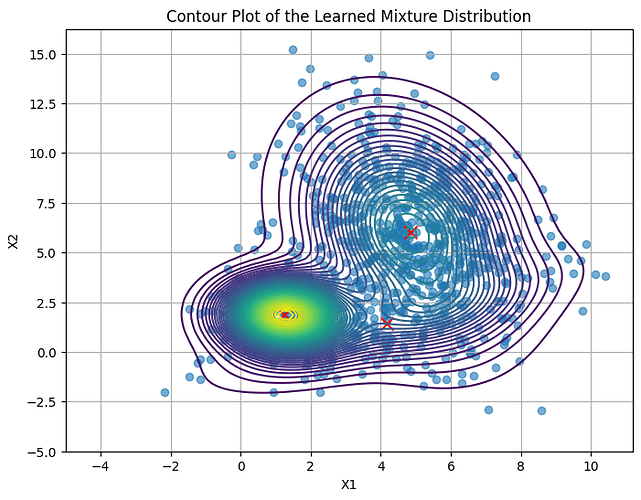
Training results: the training got stuck at a local minimum, and only one mode was learned. I think one of the reason is I defined prior distributions for z (“assignment”) and x (“obs”) in the model.

2

Hi,

You can use the same pyro.param both in the model and in the guide. For example, in your case you can use pyro.param("weights") in the model as well:

def model(data, K=3): 
    num_obs,num_dim = data.shape

    with pyro.plate("data", size=num_obs):
        assignment = pyro.sample("assignment", dist.Categorical(pyro.param("weights")))

Note, if you use the parameter both in the model and the guide then you only need to initialize it in the guide.

1 Like
3

Thank you for the suggestion, now the code works with no problems. I have to define a custom ELBO function so the parameter is penalized only once. Mu updated code:

def model(data, K=3):
    num_obs,num_dim = data.shape
    # retrieve parameters
    weights = pyro.param("weights")
    means = pyro.param("means")
    chol_factor = pyro.param("chol_factor")
    scale_diag = pyro.param("scale_diag")
    scale_tril = chol_factor @ torch.diag_embed(scale_diag)

    with pyro.plate("data", size=num_obs):
        assignment = pyro.sample("assignment", dist.Categorical(weights))  
        pyro.sample("obs", dist.MultivariateNormal(means[assignment], scale_tril=scale_tril[assignment]), obs=data)

def guide(data, K=3):
    num_obs,num_dim = data.shape
    # define learnable parameters: mixture weights, means, covariance matrices
    weights = pyro.param("weights", torch.ones(K)/K, constraint=dist.constraints.simplex)
    means = pyro.param("means", torch.randn(K, num_dim))
    chol_factor = pyro.param("chol_factor", torch.eye(num_dim).repeat(K, 1, 1))
    scale_diag = pyro.param("scale_diag", torch.ones(K, num_dim), constraint=dist.constraints.positive)
    scale_tril = chol_factor @ torch.diag_embed(scale_diag)

    with pyro.plate("data", size=num_obs):
        # log(pi_k) + log(Normal(x_i | mu_k, Sigma_k))
        log_probs = torch.stack([dist.MultivariateNormal(means[k], scale_tril=scale_tril[k]).log_prob(data) for k in range(K)], dim=-1) + torch.log(weights)
        assignment_probs = torch.exp(log_probs - torch.logsumexp(log_probs, dim=1, keepdim=True))
        assignment = pyro.sample("assignment", dist.Categorical(probs=assignment_probs))

def EM_m_step(model, guide, *args, **kwargs):
    guide_trace = pyro.poutine.trace(guide).get_trace(*args, **kwargs)
    model_trace = pyro.poutine.trace(pyro.poutine.replay(model, trace=guide_trace)).get_trace(*args, **kwargs)
    
    elbo = 0.0
    for site in model_trace.nodes.values():
        if site["type"] == "sample":
            elbo = elbo + site["fn"].log_prob(site["value"]).sum()

    return -elbo

Select the best initialization:

optim = Adam({"lr": 0.001, "betas": [0.8, 0.99]})

def initialize(seed):
    global svi
    pyro.set_rng_seed(seed)
    pyro.clear_param_store()
    svi = SVI(model, guide, optim, EM_m_step)
    return svi.loss(model, guide, samples, K=3)

# Choose the best among 100 random initializations.
loss, seed = min((initialize(seed), seed) for seed in range(100)) # only first argument, which is the loss, is being compared.
initialize(seed)
print(f"seed = {seed}, initial_loss = {loss}")

Training:

num_steps = 10000
losses = []
for step in range(num_steps):
    loss = svi.step(samples, K=3)
    losses.append(loss)

Visualization:

learned_weights = pyro.param("weights").detach()
learned_means = pyro.param("means").detach()
chol_factor = pyro.param("chol_factor").detach()
learned_scale_diag = pyro.param("scale_diag").detach()
learned_scale_tril = chol_factor @ torch.diag_embed(learned_scale_diag)

# Define grid for contour plot
x, y = np.linspace(-5, 10, 100), np.linspace(-5, 15, 100)
X, Y = np.meshgrid(x, y)
pos = np.dstack((X, Y))  # Correctly stacking X and Y for the 'pos' array

# Calculate mixture density
pdf = np.zeros(X.shape)
for i in range(learned_weights.shape[0]):
    mean = learned_means[i].numpy()
    cov = (learned_scale_tril[i] @ learned_scale_tril[i].t()).numpy()
    rv = multivariate_normal(mean=mean, cov=cov)  # Define the random variable
    pdf_component = rv.pdf(pos)  # Calculate the density for this component over the grid
    pdf += learned_weights[i].numpy() * pdf_component  # Properly scaling by the mixture weight

# Create contour plot
plt.figure(figsize=(8, 6))
plt.contour(X, Y, pdf, levels=50, cmap='viridis')
plt.scatter(samples[:, 0], samples[:, 1], alpha=0.6, label='Samples')
plt.scatter(learned_means[:, 0], learned_means[:, 1], c='r', s=100, marker='x')  # Mark the means
plt.title('Contour Plot of the Learned Mixture Distribution')
plt.xlabel('X1')
plt.ylabel('X2')
plt.grid(True)
plt.show()

gmm
gmm702×547 187 KB

Thank you Pyro development team, you guys are the BEST! Pyro is the most powerful and flexible tool I ever used. Thank you!

1 Like