Hi guys, I have a question about the best way to calculate/visualize pyro gradient norms throughout training.
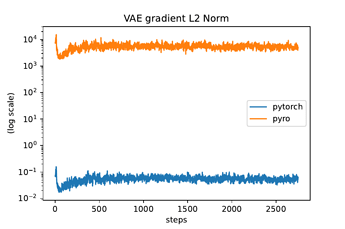
I used the pyro example code (pyro/vae_comparison.py at dev · pyro-ppl/pyro · GitHub), which contains a comparable Pyro/Pytorch implementation of a simple VAE, and recorded the L2 norm of the gradients at each step using the get_grad_norm() method in the code block below.
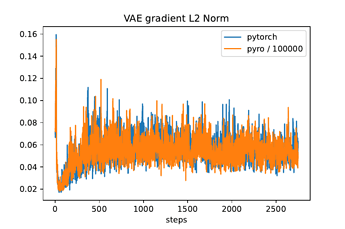
The way I’m doing it leads to pyro gradient norms being scaled by 100000 compared to the pytorch version (see figures below), but I don’t know why?
# Copyright (c) 2017-2019 Uber Technologies, Inc.
# SPDX-License-Identifier: Apache-2.0
import argparse
import itertools
import os
from abc import ABCMeta, abstractmethod
import torch
import torch.nn as nn
from torch.nn import functional
from torchvision.utils import save_image
from mnist_cached import DATA_DIR, RESULTS_DIR
import pyro
from pyro.contrib.examples import util
from pyro.distributions import Bernoulli, Normal
from pyro.infer import SVI, JitTrace_ELBO, Trace_ELBO
from pyro.optim import Adam
"""
Comparison of VAE implementation in PyTorch and Pyro. This example can be
used for profiling purposes.
The PyTorch VAE example is taken (with minor modification) from pytorch/examples.
Source: https://github.com/pytorch/examples/tree/master/vae
"""
TRAIN = "train"
TEST = "test"
OUTPUT_DIR = RESULTS_DIR
# VAE encoder network
class Encoder(nn.Module):
def __init__(self):
super().__init__()
self.fc1 = nn.Linear(784, 400)
self.fc21 = nn.Linear(400, 20)
self.fc22 = nn.Linear(400, 20)
self.relu = nn.ReLU()
def forward(self, x):
x = x.reshape(-1, 784)
h1 = self.relu(self.fc1(x))
return self.fc21(h1), torch.exp(self.fc22(h1))
# VAE Decoder network
class Decoder(nn.Module):
def __init__(self):
super().__init__()
self.fc3 = nn.Linear(20, 400)
self.fc4 = nn.Linear(400, 784)
self.relu = nn.ReLU()
def forward(self, z):
h3 = self.relu(self.fc3(z))
return torch.sigmoid(self.fc4(h3))
class VAE(object, metaclass=ABCMeta):
"""
Abstract class for the variational auto-encoder. The abstract method
for training the network is implemented by subclasses.
"""
def __init__(self, args, train_loader, test_loader):
self.args = args
self.vae_encoder = Encoder()
self.vae_decoder = Decoder()
self.train_loader = train_loader
self.test_loader = test_loader
self.mode = TRAIN
def set_train(self, is_train=True):
if is_train:
self.mode = TRAIN
self.vae_encoder.train()
self.vae_decoder.train()
else:
self.mode = TEST
self.vae_encoder.eval()
self.vae_decoder.eval()
@abstractmethod
def compute_loss_and_gradient(self, x):
"""
Given a batch of data `x`, run the optimizer (backpropagate the gradient),
and return the computed loss.
:param x: batch of data or a single datum (MNIST image).
:return: loss computed on the data batch.
"""
return
def model_eval(self, x):
"""
Given a batch of data `x`, run it through the trained VAE network to get
the reconstructed image.
:param x: batch of data or a single datum (MNIST image).
:return: reconstructed image, and the latent z's mean and variance.
"""
z_mean, z_var = self.vae_encoder(x)
if self.mode == TRAIN:
z = Normal(z_mean, z_var.sqrt()).rsample()
else:
z = z_mean
return self.vae_decoder(z), z_mean, z_var
def train(self, epoch):
self.set_train(is_train=True)
train_loss = 0
for batch_idx, (x, _) in enumerate(self.train_loader):
loss = self.compute_loss_and_gradient(x)
train_loss += loss
print(
"====> Epoch: {} \nTraining loss: {:.4f}".format(
epoch, train_loss / len(self.train_loader.dataset)
)
)
def test(self, epoch):
self.set_train(is_train=False)
test_loss = 0
for i, (x, _) in enumerate(self.test_loader):
with torch.no_grad():
recon_x = self.model_eval(x)[0]
test_loss += self.compute_loss_and_gradient(x)
if i == 0:
n = min(x.size(0), 8)
comparison = torch.cat(
[x[:n], recon_x.reshape(self.args.batch_size, 1, 28, 28)[:n]]
)
save_image(
comparison.detach().cpu(),
os.path.join(OUTPUT_DIR, "reconstruction_" + str(epoch) + ".png"),
nrow=n,
)
test_loss /= len(self.test_loader.dataset)
print("Test set loss: {:.4f}".format(test_loss))
class PyTorchVAEImpl(VAE):
"""
Adapted from pytorch/examples.
Source: https://github.com/pytorch/examples/tree/master/vae
"""
def __init__(self, *args, **kwargs):
super().__init__(*args, **kwargs)
self.optimizer = self.initialize_optimizer(lr=1e-3)
def compute_loss_and_gradient(self, x):
self.optimizer.zero_grad()
recon_x, z_mean, z_var = self.model_eval(x)
binary_cross_entropy = functional.binary_cross_entropy(
recon_x, x.reshape(-1, 784)
)
# Uses analytical KL divergence expression for D_kl(q(z|x) || p(z))
# Refer to Appendix B from VAE paper:
# Kingma and Welling. Auto-Encoding Variational Bayes. ICLR, 2014
# (https://arxiv.org/abs/1312.6114)
kl_div = -0.5 * torch.sum(1 + z_var.log() - z_mean.pow(2) - z_var)
kl_div /= self.args.batch_size * 784
loss = binary_cross_entropy + kl_div
if self.mode == TRAIN:
loss.backward()
model_params = itertools.chain(
self.vae_encoder.named_parameters(), self.vae_decoder.named_parameters()
)
print(get_grad_norm(model_params))
self.optimizer.step()
return loss.item()
def initialize_optimizer(self, lr=1e-3):
model_params = itertools.chain(
self.vae_encoder.parameters(), self.vae_decoder.parameters()
)
return torch.optim.Adam(model_params, lr)
class PyroVAEImpl(VAE):
"""
Implementation of VAE using Pyro. Only the model and the guide specification
is needed to run the optimizer (the objective function does not need to be
specified as in the PyTorch implementation).
"""
def __init__(self, *args, **kwargs):
super().__init__(*args, **kwargs)
# self.optimizer = self.initialize_optimizer(lr=1e-3)
self.optimizer, self.loss_fn = self.initialize_optimizer(lr=1e-3)
def model(self, data):
decoder = pyro.module("decoder", self.vae_decoder)
z_mean, z_std = torch.zeros([data.size(0), 20]), torch.ones([data.size(0), 20])
with pyro.plate("data", data.size(0)):
z = pyro.sample("latent", Normal(z_mean, z_std).to_event(1))
img = decoder.forward(z)
pyro.sample(
"obs",
Bernoulli(img, validate_args=False).to_event(1),
obs=data.reshape(-1, 784),
)
def guide(self, data):
encoder = pyro.module("encoder", self.vae_encoder)
with pyro.plate("data", data.size(0)):
z_mean, z_var = encoder.forward(data)
pyro.sample("latent", Normal(z_mean, z_var.sqrt()).to_event(1))
def compute_loss_and_gradient(self, x):
if self.mode == TRAIN:
# loss = self.optimizer.step(x)
loss = self.loss_fn(self.model, self.guide, x)
loss.backward()
model_params = itertools.chain(
self.vae_encoder.named_parameters(), self.vae_decoder.named_parameters()
)
print(get_grad_norm(model_params))
self.optimizer.step()
self.optimizer.zero_grad()
else:
# loss = self.optimizer.evaluate_loss(x)
with torch.no_grad():
loss = self.loss_fn(self.model, self.guide, x)
# loss /= self.args.batch_size * 784
loss = loss.item() / self.args.batch_size * 784
return loss
def initialize_optimizer(self, lr):
# optimizer = Adam({"lr": lr})
# elbo = JitTrace_ELBO() if self.args.jit else Trace_ELBO()
# return SVI(self.model, self.guide, optimizer, loss=elbo)
model_params = itertools.chain(
self.vae_encoder.parameters(), self.vae_decoder.parameters()
)
optimizer = torch.optim.Adam(model_params, lr)
loss_fn = JitTrace_ELBO().differentiable_loss if self.args.jit else Trace_ELBO().differentiable_loss
return optimizer, loss_fn
def setup(args):
pyro.set_rng_seed(args.rng_seed)
train_loader = util.get_data_loader(
dataset_name="MNIST",
data_dir=DATA_DIR,
batch_size=args.batch_size,
is_training_set=True,
shuffle=True,
)
test_loader = util.get_data_loader(
dataset_name="MNIST",
data_dir=DATA_DIR,
batch_size=args.batch_size,
is_training_set=False,
shuffle=True,
)
global OUTPUT_DIR
OUTPUT_DIR = os.path.join(RESULTS_DIR, args.impl)
if not os.path.exists(OUTPUT_DIR):
os.makedirs(OUTPUT_DIR)
pyro.clear_param_store()
return train_loader, test_loader
def get_grad_norm(model_params):
norm = 0
for _, p in model_params:
try:
norm += torch.linalg.norm(p.grad.detach().data).item()**2
except:
pass
return norm**0.5
def main(args):
pyro.enable_validation(False)
train_loader, test_loader = setup(args)
if args.impl == "pyro":
vae = PyroVAEImpl(args, train_loader, test_loader)
print("Running Pyro VAE implementation")
elif args.impl == "pytorch":
vae = PyTorchVAEImpl(args, train_loader, test_loader)
print("Running PyTorch VAE implementation")
else:
raise ValueError("Incorrect implementation specified: {}".format(args.impl))
for i in range(args.num_epochs):
vae.train(i)
if not args.skip_eval:
vae.test(i)
if __name__ == "__main__":
assert pyro.__version__.startswith("1.7.0")
parser = argparse.ArgumentParser(description="VAE using MNIST dataset")
parser.add_argument("-n", "--num-epochs", nargs="?", default=10, type=int)
parser.add_argument("--batch_size", nargs="?", default=128, type=int)
parser.add_argument("--rng_seed", nargs="?", default=0, type=int)
parser.add_argument("--impl", nargs="?", default="pyro", type=str)
parser.add_argument("--skip_eval", action="store_true")
parser.add_argument("--jit", action="store_true")
parser.set_defaults(skip_eval=False)
args = parser.parse_known_args()[0]
main(args)
If there’s a better/more general way of doing this such that I can retrieve gradient norms from pyro that are the same as pytorch (without scaling by 100000) please let me know, thanks!