Hi,
For a project at university, I’m building a relatively large probabilistic model inspired by a multilayer perceptron. The architecture of my MLP is the following: [784, 128, 64, 10]. So, the weight matrices are shaped as follows: [(784, 128), (128, 64), (64,10)]. My model stipulates that columnar weights are conditionally independent of each other.
I think that I’ve successfully managed to define the model function using Pyro and insuring conditional independence of weights across layers as I perceive it. The main idea of the graph structure is that activations of a given layer are defined as latent variables, and these activations are dependent on the column weights of the weight matrix of the previous layer and the activations of the previous layer. What we get, as you may have guessed, is some sort of a hierarchical model.
My goal is to pass in datasets of MLPs (in a layerwise fashion) through this probabilistic model, run SVI on it and sample weights from its posterior distribution. The code hereunder shows the way I defined my model using plates and defining independent dimensions.
def mlp_pgm_final(
weight_layer_dataset: list[torch.Tensor] = None,
bias_layer_dataset: list[torch.Tensor] = None,
):
dataset_len = weight_layer_dataset[0].size()[0] if weight_layer_dataset else 1
layer_structure = (784, 128, 64, 10)
weight_matrix_dims = [
(layer_structure[i], layer_structure[i + 1])
for i in range(len(layer_structure) - 1)
]
bias_dims = [(layer_structure[k], 1) for k in range(1, len(layer_structure))]
# print(weight_matrix_dims)
x = torch.randn(dataset_len, 784, 1)
layer_idx = 0
activations = []
for _ in range(len(weight_matrix_dims)): # iterate over number of weight matrices
upper_bound = (1 / layer_structure[layer_idx]) ** (1 / 2) * torch.ones(
layer_structure[layer_idx]
)
lower_bound = (
-upper_bound
) # define lower and upper bound for uniform distributions used to initialise weights for NNs
# print(upper_bound[0])
b_upper_bound = (1 / layer_structure[layer_idx + 1] ** (1 / 2)) * torch.ones(
layer_structure[layer_idx + 1]
)
b_lower_bound = -b_upper_bound
# print(b_lower_bound[0])
with pyro.plate(f"Layer_{layer_idx+1}", dataset_len, dim=-3):
# print(layer_idx)
b = pyro.sample(
f"b_{layer_idx+1}",
dist.Uniform(b_lower_bound, b_upper_bound),
obs=bias_layer_dataset[layer_idx] if bias_layer_dataset else None,
) # Sample b vector from uniform
# w = torch.empty(weight_matrix_dims[layer_idx]) # create placeholder tensor for weights so that we can concatenate independent variational parameters to do weight multiplication
# for j in range(weight_matrix_dims[layer_idx][1])
with pyro.plate(
f"Layer_Weights_{layer_idx+1}", weight_matrix_dims[layer_idx][1], dim=-2
) as j:
# print(weight_layer_dataset[layer_idx].size())
w = pyro.sample(
f"w_{layer_idx+1}",
dist.Uniform(lower_bound, upper_bound),
obs=weight_layer_dataset[layer_idx]
if weight_layer_dataset
else None,
)
if weight_layer_dataset:
# print("Layer %d, Bias %s, Weight %s, Input %s" % (layer_idx+1, b.size(), w.size(), x.size()))
act = torch.relu(torch.matmul(w.mT, x) + b.unsqueeze(-1))
else:
b = b.permute(0, 2, 1).squeeze(-1)
# print("Layer %d, Bias %s, Weight %s, Input %s" % (layer_idx+1, b.size(), w.size(), x.size()))
# print(torch.matmul(x.squeeze(), w.mT).size())
act = torch.relu(torch.matmul(x.squeeze(), w.mT) + b).squeeze()
# print("Layer %d, Bias %s, Weight %s, Act %s" % (layer_idx+1, b.size(), w.size(), act.size()))
# activations.append(act)
# cov = torch.eye(act.size(1))
with pyro.plate(f"Activations_{layer_idx+1}", 1, dim=-3):
cov = torch.stack(
[torch.eye(bias_dims[layer_idx][0]) for _ in range(act.size()[0])],
dim=0,
)
h_dist = dist.MultivariateNormal(act.squeeze(), cov)
# print("Test Sample size", h_dist.sample().size())
h = pyro.sample(f"h_{layer_idx +1}", h_dist).squeeze()
# print("Latent Sample", h.size())
x = h.unsqueeze(-1)
layer_idx += 1
With this model definition, I’ve been facing a couple of problems that have left me perplexed.
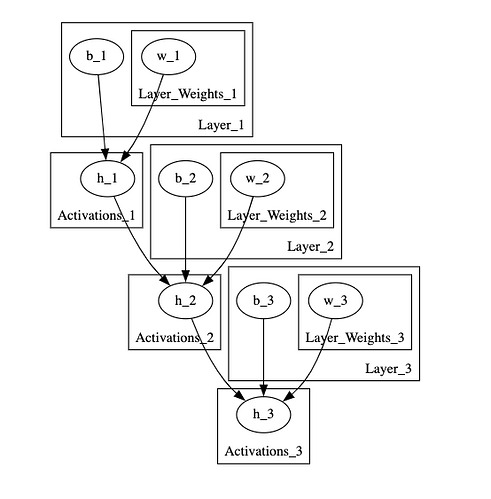
First, when I want to visualise the model that I have defined using the pyro.render() method, I get a tensor dimension RunTime error preventing me from visualising my model when I have observations passed as arguments to the model. I’ve checked and double-checked that my dimensions are correct, this error just doesn’t make sense. And interestingly, when passing “None” as my model arguments the model rendering works fine. My model also passes the test_model() method found in the tensor shapes pyro tutorial. This is what my graphical model looks like:
The second issue, which is more interesting, is that when running a very standard SVI loop on this model, with a dataset size of 1 or 2 MLP samples, my program simply crashes. My strongest suspicion is that this is due to the fact that my graph is very high-dimensional (first layer has 128 conditionally independent variables all related to the next layer’s activation and so on) and that the memory requirements are simply too great.
Could any of you help me find the flaws in my approach and perhaps help me solve this problem?
Thanks in advance!