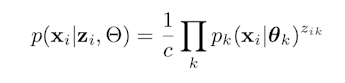Product of exponential family distributions

1

Hi,

I’m interested in implementing the finite version of the Infinite Overlapping Mixture Model paper by Heller and Ghahramani (http://mlg.eng.cam.ac.uk/zoubin/papers/HelGha07over.pdf) where the mixture model is defined as follows:

image
image730×176 5.27 KB

Here, unlike typical mixture models, the mixture is defined as a product of k components that belong to the exponential family. z_ik is a binary vector (which might have multiple 1s) and c is the normalization constant. (Note that this is not same as the product of random variables)

I’m thinking of possible ways to do this in Pyro, but before that, I’d like to show you also the derivation of this product for exponential family distributions. As authors state in the paper:

image
image1192×1050 76.8 KB

Product of exp. fam. distributions is a new distribution of the same family with a natural parameter that is the sum of the natural parameters of the components. Now I wonder if this can be elegantly implemented in Pyro.

I’m not familiar with Pyro but I think it’s very cool that all exp.fam. distributions in PyTorch have _natural_params property which I can use for this purpose, however, this property uses “native” parameters of the distributions e.g. self.loc and self.scale in the Normal case and self.probs in the Bernoulli case.

I can write classes for the distributions I need by inheriting from existing classes of Pyro, but I was wondering if there is an easier way to define a generic class like ProductDistribution which takes a list of exp.fam. distribution objects and behaves like the product I mentioned above.

Any ideas?

1 Like
2

Hi @gkcn, interesting observation! One clean way to implement this would be to define an abstract static method

class ExponentialFamily(Distribution):
    @staticmethod
    def _from_natural_params(*params):
        raise NotImplementedError

and provide implementations for all the ExponentialFamily distributions, e.g.

class Normal(Distribution):
    @staticmethod
    def _from_natural_params(m1, m2):
        loc = (-0.5) * m1 / m2
        scale = (m2 * (-2)).rsqrt()
        return Normal(loc, scale)

Once you’ve defined this, you can create a method for batched ExponentialFamily distributions

class ExponentialFamily(Distribution):
    def product_along_axis(self, dim=-1, keepdim=True):
        if dim >= 0:
            dim = dim - len(self.batch_shape) - 1
        dim = dim - len(self.event_shape)
        params = self._natural_params()
        params = [p.sum(dim, keepdim=keepdim) for p in params]
        return self._from_natural_params(*params)

Actually we already implement this in Funsor as the .reduce(ops.add, -) method in log space, and we use this for e.g. fusing a batch of observations along a plate dimension.

3

Thanks so much for the reply @fritzo! I have just sent a PR (Add _from_natural_params and product_along_axis function to ExponentialFamily class by gokceneraslan · Pull Request #32177 · pytorch/pytorch · GitHub) and tagged you.