I’m trying to do variational inference for a stochastic volatility model. It’s Model 2 on page 365 in this paper if interested. I’m new to pyro, so I don’t really have any idea what I’m doing, but I cannot get this to cooperate. I made it up in Stan and did MCMC no problem, so I know there are viable parameters.
‘returns’ is a 2271x3 matrix and ‘corr_mat’ is a 3x3 correlation matrix.
This is the model:
def model(returns, corr):
T = returns.shape[0]
y = returns.shape[1]
with pyro.plate('params', y):
mu = pyro.sample('mu', dist.Normal(0, 25))
phi = pyro.sample('phi', dist.Uniform(-1, 1))
sigma = pyro.sample('sigma', dist.HalfCauchy(5))
h = torch.empty((T, y))
# Volatility is a one period markov process
for t in pyro.poutine.markov(range(T)):
if t == 0:
h[t] = pyro.sample(f'h_{t}', dist.Normal(mu, sigma).to_event(1))
else:
h[t] = pyro.sample(f'h_{t}', dist.Normal(mu + phi * (h[t - 1] - mu), sigma).to_event(1))
# Returns are condtionally independent across time given volatility h
for t in pyro.plate('ret_proc', T):
# Cholesky of covariance matrix = diagonal matrix of sigmas * cholesky of correlation matrix
pyro.sample(f'r_{t}', dist.MultivariateNormal(torch.zeros(y), scale_tril=torch.exp(h[t] / 2).diag() @ corr),
obs=returns[t])
And this is the RNN I’m trying use to amortize the guide:
class RNNTransform(torch.nn.Module):
def __init__(self, input_size, output_size):
"""
Transforms RNN output into location and scale parameters for sampling
"""
super().__init__()
self.loc_trans = torch.nn.Linear(input_size, output_size)
self.scale_trans = torch.nn.Linear(input_size, output_size)
self.softplus = torch.nn.Softplus()
def forward(self, rnn_out):
loc_params = self.loc_trans(rnn_out)
# Softplus ensures positivity for scale parameter
scale_params = self.softplus(self.scale_trans(rnn_out))
return loc_params, scale_params
class RNNGuide(torch.nn.Module):
def __init__(self, length, tickers):
"""
Uses RNN to amortize returns matrix for variational inference
"""
super().__init__()
# Trainable intial RNN state
self.r_0 = torch.nn.Parameter(torch.zeros(1, 1, 5))
self.rnn = torch.nn.RNN(input_size=tickers, hidden_size=5)
self.rnn_trans = RNNTransform(5, 1)
def guide(self, returns, corr):
pyro.module('rnn', self)
T = returns.shape[0]
y = returns.shape[1]
rnn_out, _ = self.rnn(returns.unsqueeze(1), self.r_0)
loc, scale = self.rnn_trans(rnn_out)
for t in range(T):
pyro.sample(f'h_{t}', dist.Normal(loc[t], scale[t]).to_event(1))
Here’s the training loop:
adam_params = {"lr": .1, "betas": (0.90, 0.999)}
optimizer = Adam(adam_params)
svi = SVI(model, guide, optimizer, loss=Trace_ELBO())
losses = []
n_steps = 25
for step in range(n_steps):
loss = svi.step(returns, corr_mat)
losses.append(loss)
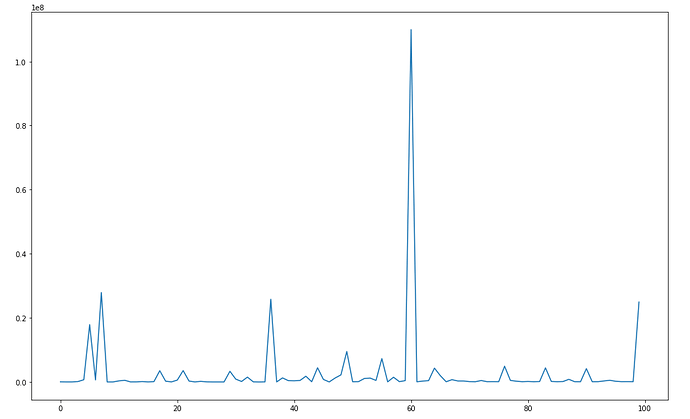
When I run this, the losses look like this:
Any help or advice would be appreciated. I honestly don’t know enough about this to properly diagnose the problem, so even some words of where to look would be nice.