Problem in Implementing a PGM

Misc.
1

Hi everyone, I am struggling with this problem for more than a week now and I will appreciate ANY help and suggestions.

I am trying to implement this graphical model:
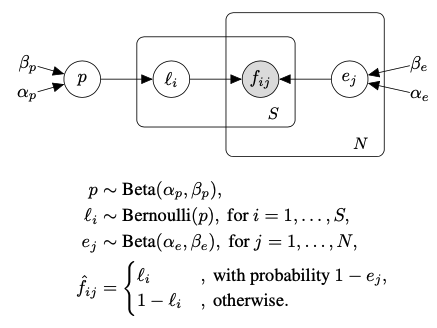
Screen Shot 2021-01-20 at 6.58.32 PM

My implementation is:

def model(data): 
    p = pyro.sample('p', dist.Beta(1, 1))

    label_axis = pyro.plate("label_axis", data.shape[0], dim=-3)
    f_axis = pyro.plate("f_axis", data.shape[1], dim=-2)

    with label_axis:
        l = pyro.sample('l', dist.Bernoulli(p))
    
    with f_axis:
        e = pyro.sample('e', dist.Beta(1, 10))

    with label_axis, f_axis:
        f = pyro.sample('f', dist.Bernoulli(1-e), obs=data)
        f = l*f + (1-l)*(1-f)
     return f

However, this doesn’t seem to be right to me. The problem is “f”. Since its distribution is different from Bernoulli. To sample from f, I used a sample from a Bernoulli distribution and then changed the sampled value if l=0. But I don’t think that this would change the value that Pyro stores behind the scene for “f”. This would be a problem when it’s inferencing, right?

I wanted to use iterative plates instead of vectorized one, to be able to use control statements inside my plate. But apparently, this is not possible since I am reusing plates.

How can I correctly implement this PGM? Do I need to write a custom distribution? Or can I hack Pyro and change the stored value for “f” myself? Any type of help is appreciated! Cheers!

2

@arashkhoeini You can define the likelihood as

prob = l * (1 - e) + (1 - l) * e
return pyro.sample('f', dist.Bernoulli(prob), obs=data)

where prob is the probably to get f=1.

3

Thank you @fehiepsi! Just a naive question: Wouldn’t this implementation mess with plates and conditional independence?

4

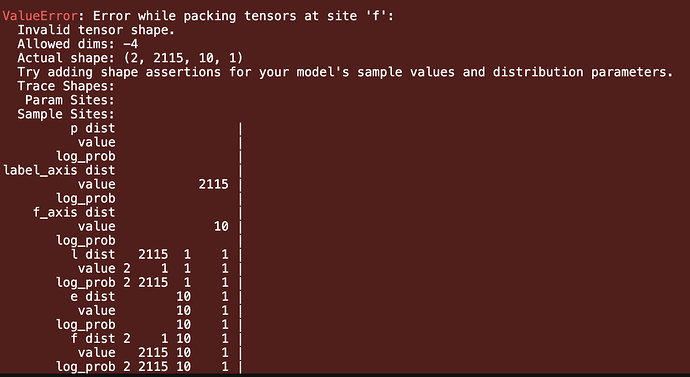
I tried it and now I get this error during MCMC using NUTZ kernel. Any idea? data shape is (2115, 10)

Screen Shot 2021-01-20 at 9.50.17 PM
Screen Shot 2021-01-20 at 9.50.17 PM1574×860 87.1 KB

5

Hi @arashkhoeini with that data, you should put label axis on dim -2 and f axis on dim -1.

6

I am sorry that I am asking way too many questions @fehiepsi !

I changed the dimensions as you mentioned. It works fine when I sample from my model. But I encounter this error when I run MCMC on it: RuntimeError: The size of tensor a (2) must match the size of tensor b (2115) at non-singleton dimension 0

I also print the shape of ‘l’ and ‘e’ during the inference and I saw something that I don’t understand:
l : (2115, 1)
e: (10)
l: (2, 1, 1)
e: (10)

Why does the shape of ‘e’ changes to (2, 1, 1) in the second iteration?

I really appreciate your help!

7

I am not sure why. Your model works in my system

import pyro
import pyro.distributions as dist
from pyro.infer import MCMC, NUTS

def model(data): 
    p = pyro.sample('p', dist.Beta(1, 1))

    label_axis = pyro.plate("label_axis", data.shape[0], dim=-2)
    f_axis = pyro.plate("f_axis", data.shape[1], dim=-1)

    with label_axis:
        l = pyro.sample('l', dist.Bernoulli(p))
    
    with f_axis:
        e = pyro.sample('e', dist.Beta(1, 10))

    with label_axis, f_axis:
        prob = l * (1 - e) + (1 - l) * e
        return pyro.sample('f', dist.Bernoulli(prob), obs=data)

mcmc = MCMC(NUTS(model), 500, 500)
data = dist.Bernoulli(0.5).sample((20, 4))
mcmc.run(data)

Pyro uses enumeration to integrate out the discrete latent variable l. The shape (2, 1, 1) just confirms that enumeration works. You can find detailed explanation about enumeration in this tutorial.

8

I was making a dumb mistake. You are a legend! Thank you very much!

I have one more question! Based on the example in MCMC doc page, mcmc.run() should return an object. But all I get is None. Do you have any idea what is that?

9

Oops, you are referring the very old docs. The latest Pyro version is 1.3.1. See the stable docs.

1 Like