Hey everyone,
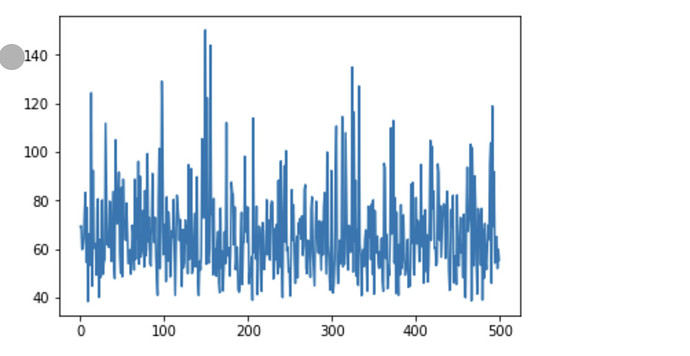
I’m kind of new here. I really like the framework but struggled to understand how to use it properly. I’m implementing a simple conjugate prior between Dirichlet distribution and categorical distribution like the conjugate prior implementation between Beta distribution and Bernoulli distribution shown in the tutorial. But the code doesn’t work, because the loss doesn’t converge at all as shown in the plot. I have tried to change the learning rate but that doesn’t help.
My code and the plot of loss during the training are attached below. Can someone help me understand what I did wrong? Thanks in advance.
pyro.clear_param_store()
d = []
for i in [1,2,3,2,1,0,0,1,5,6,7,1,1,1,2,3,1,1,1,1,1,2,2,2]:
d.append(torch.tensor(i))
data = torch.tensor(d)
def model(data):
prior = torch.ones(8)
theta1 = pyro.sample('theta1',dist.Dirichlet(prior))
with pyro.plate('observation', data.shape[0]):
pyro.sample('obs',dist.Categorical(theta1),obs=data)
def guide(data):
theta1 = pyro.param('theta1_q',torch.ones(8) ,constraint = constraints.positive)
pyro.sample('theta1',dist.Dirichlet(theta1))
n_steps = 500
adam_params = {"lr": 0.00001,"betas": (0.90, 0.999)}
optimizer = Adam(adam_params)
# setup the inference algorithm
svi = SVI(model, guide, optimizer, loss=Trace_ELBO())
losses = []
for idx in range(n_steps):
losses.append(svi.step(data))
# grab the learned variational parameters
alpha_q = pyro.param("theta1_q")
Print(alpha_q)
plt.plot(losses)