Hello,
I would like to ask for comments if/how pyro could be helpful in the following problem:
I have data from a factory producing cart parts. It describes operations needed to be done on a semi-finished product in order to be finished.
For each semi-finished product there is a list of subsequent operations needed to be performed on the product in order to become finished. One operation can be performed on one or more machines. Performing an operation wear out tools used by the machine to perform the action, e.g. if the machine is a drill, with every hole drilled by it the drill bit is being worn out. When tool is completely worn out, it must be replaced.
The task is to compute the cost of one operation on one product performed by one particular machine. Cost is a sum of all tools (e.g. drill bits) used in the operation.
Inputs are aggregated how many products of each type was manufactured and how many tools of each kind was used.
What make is difficult is the fact that when one operation can be performed on two or more machines, there is now data what portion was performed on what machine.
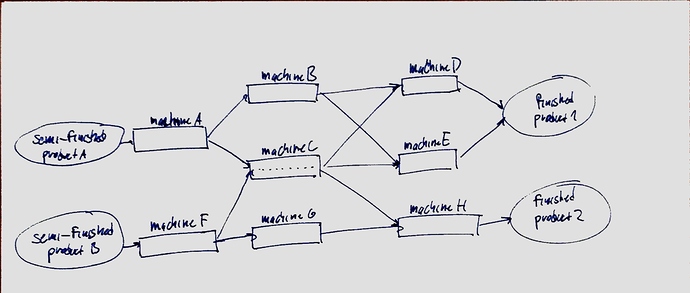
In effort to make it more clear I attached a scribble describing one of the simpler configurations.
It shows that first operation on product A can be performed only on machine A. But next operation can be done on both machine B or machine C and we don’t know what portion of outputs from machine A were sent to machine B and what portion to machine C. Machine B and machine C use different tools which have different purchasing costs and different durability so the cost of performing the same operation on different machines varies.
All outputs from both machines B,C can then be sent to both machine D and E and we again don’t know what portion was sent to D and what portion to E.
Moreover, unknown portion of second action on product B can be performed in machine C which also performs unknown portion of second actions on product A.
Some of the tools present in a machine all used in all operations, some only in particular operations, e.g. some drill bits present in machine C could be used only when performing an operation on product A , some exclusively on product B and some both.
The situation was much easier in previous years when one operation was almost exclusively done only in one machine. From that data I could compute durability of some tools and use it as priors in the more complicated above described case.
Would you tell that such a problem can by tackled by probabilistic programming?