Probabilistic Programming and Bayesian Methods for Hackers

Tutorials
1

Hi,
Just started learning Probabilistic Programming, and as I come from PyTorch, would love to learn Pyro instead of PyMC3 or TFP.
I started by reading Probabilistic Programming and Bayesian Methods for Hackers and porting the code.

Right at the end of the chapter 1, there’s a part of the model that I’m finding very hard to implement. It is the switchpoint:
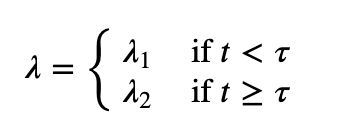
Screen Shot 2020-08-10 at 21.07.55

In PyMC3, that is achieved in a single line:

lambda_ = pm.math.switch(tau > idx, lambda_1, lambda_2)

In TFP, the following lines do the job:

lambda_ = tf.gather(
         [lambda_1, lambda_2],
         indices=tf.cast(tau * tf.cast(tf.size(count_data), dtype=tf.float32) <= tf.cast(tf.range(tf.size(count_data)), dtype=tf.float32), dtype=tf.int32))

In Pyro, I thought about 2 ways of doing it. The first, unvectorized:

tau = pyro.sample("tau", dist.Uniform(0, 1))
tau = (n_count_data * tau).int()
for i in pyro.plate("data_loop", len(count_data)):
    if i <= tau:
        pyro.sample("obs_{}".format(i), dist.Poisson(lambda_1), obs=count_data[i])
    else:
        pyro.sample("obs_{}".format(i), dist.Poisson(lambda_2), obs=count_data[i])

which is obviously extremely slow.

The other, the vectorized way, to my surprise was even slower than the unvectorized:

with pyro.plate("data_loop_1", tau):
    pyro.sample("obs1", dist.Poisson(lambda_1), obs=count_data[:tau])
   
with pyro.plate("data_loop_2", n_count_data - tau):
    pyro.sample("obs2", dist.Poisson(lambda_2), obs=count_data[tau:])

Why this last vectorized way is slower than the naive loop?
But most important: how to implement this swichpoint properly in Pyro?

Thanks!

1 Like
2

@carlossouza I think you can use torch.where here. We have a similar model in numpyro where we use np.where.

Edit: I just found an old gist which uses torch.expand and torch.cat.

2 Likes
3

Thanks, worked perfectly! Here’s the final port of Chapter 1 to Pyro.

I created a PR on the book’s repository, so that it will include not only PyMC2/3, Tensorflow Probability, but also Pyro. Also created a PR to include in Pyro’s tutorials.

I believe these introductory materials can significantly increase the adoption of the language.

Thanks again!

5 Likes