Suppose you know that your data come from a Gaussian mixture, and you know both the frequencies of the components and the locations and scales of each component. Suppose that the only thing you’re trying to infer is the cluster assignments of new data.
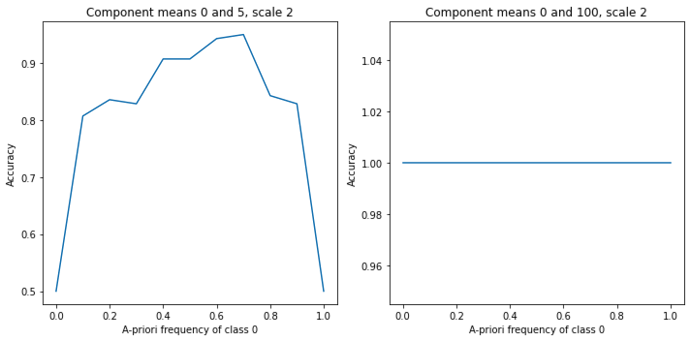
I have found that in this scenario, even if you specify a very low frequency for one of the components, data from that component (not necessarily appearing in the dataset with the same frequency that you specify) are often correctly classified. This is not strange, especially if the components are quite separated.
Intuitively, though, you should be able to push the a-priori frequency low enough, e.g. to 0, so that no further classification into the low-frequency bucket occurs. In theory, an a-priori frequency of 0 for a class corresponds to a term of negative infinity in the log likelihood for assignments to that class.
I have noticed that when using @infer_discrete, I still get classifications in the low-frequency bucket even when I stipulate that the low-frequency class occurs with probability 0. Is my idea of what occurs in MAP inference misguided?
Here is the code (lightly adapted from the GMM tutorial) that I have been using to produce this behavior. Note that the clusters are cleanly separated (means 0 and 100, scale 2), everything except the assignments is known a-priori, and by default class 0 has a-priori frequency 0 but we still correctly classify 100% of its (70) members in the dataset (n=140).
import torch
import numpy as np
import pyro
import pyro.distributions as dist
from pyro import poutine
from pyro.infer.autoguide import AutoDelta
from pyro.infer import config_enumerate, infer_discrete
# generate synthetic data
n_0 = 70
n_1 = 70
# widely separated components
locs = torch.tensor([0., 100.])
scale = 2.
# frequency of class 0 is 0 by default
freq = 0
freqs = torch.tensor([freq, 1 - freq])
data = torch.tensor(np.random.normal(loc=locs[0],scale=scale,size=n_0).tolist() +
np.random.normal(loc=locs[1],scale=scale,size=n_1).tolist())
ids = torch.tensor([0 for _ in range(n_0)] + [1 for _ in range(n_1)])
@config_enumerate
def model(data):
with pyro.plate('data', len(data)):
# Local variables.
assignment = pyro.sample('assignment', dist.Categorical(probs=freqs))
pyro.sample('obs', dist.Normal(locs[assignment], scale), obs=data)
global_guide = AutoDelta(poutine.block(model))
guide_trace = poutine.trace(global_guide).get_trace(data) # record the globals
trained_model = poutine.replay(model, trace=guide_trace) # replay the globals
def classifier(data, temperature=0):
inferred_model = infer_discrete(trained_model, temperature=temperature,
first_available_dim=-2) # avoid conflict with data plate
trace = poutine.trace(inferred_model).get_trace(data)
return trace.nodes["assignment"]["value"]
# accuracy is 100% - inspecting `preds` shows that we predict 70 members of class 0
# (the class with frequency 0)
preds = classifier(data)
acc = sum(preds.squeeze() == ids.squeeze()) / len(ids.squeeze())
print(acc)
If the clusters are not as drastically separated, then I observe the expected behavior. Namely, accuracy goes up when the a-priori frequency is close to the true frequency, and down otherwise.