Piecewise regression with TraceEnum_ELBO

Misc.
1

Hello Pyro experts,

I’m trying to implement a piecewise linear regression model. I’ve tried various variations on the model, but I haven’t been able to get good results. My approach is to sample change points from a Categorical and use a MaskedMixture with a linear regression as one component distribution, and another MaskedMixture as the other component (i.e. the MaskedMixture’s are nested as many times as there are pieces).

def piecewise_regression(x, y, n_pieces = 3):
    """
    piecewise regression where pieces are connected and the last piece has slope 0
    """
    N = x.shape[0]
    lines = []
    change_points = []
    line_distributions = []
    for piece in pyro.plate('pieces', n_pieces):
        if piece == 0:
            lines.append(sample_linear_regression())
            line_distributions.append(dist.Normal(lines[-1][0]*x+lines[-1][1],lines[-1][2]))
            change_point = sample_change_point(x, piece)
            change_points.append(change_point)
        elif piece < n_pieces-1:
            mask = torch.arange(N) > change_points[-1]
            slope, noise_std = sample_slope_and_noise_std(piece)
            prev_slope = lines[-1][0]
            prev_intercept = lines[-1][1]
            intercept = (prev_slope*x[change_point]+prev_intercept)-slope*x[change_point]
            lines.append((slope,intercept,noise_std))
            prev_dist = line_distributions[-1]
            line_distributions.append(dist.MaskedMixture(mask, prev_dist, dist.Normal(lines[-1][0]*x+lines[-1][1],lines[-1][2])))
            # if all of x is masked, sample_change_point returns the last x
            change_point = sample_change_point(x, piece)
            change_point = min(change_point + change_points[-1], N)
            change_points.append(change_point)
        else:
            noise_std = pyro.sample('noise_std_{}'.format(piece), dist.LogNormal(0.,1.))
            intercept = lines[-1][0]*x[change_points[-1]]+lines[-1][1]
            lines.append((intercept,noise_std))
            prev_dist = line_distributions[-1]
            last_mask = torch.arange(N) >= change_points[-1]
            line_distributions.append(dist.MaskedMixture(last_mask, prev_dist, dist.Normal(lines[-1][0],lines[-1][1])))
    with pyro.plate('N', N):
        y = pyro.sample("obs", line_distributions[-1], obs=y)
    return y, lines, change_points, line_distributions

def sample_change_point(x, piece, mask = None):
    n_iter = x.shape[0]
    if mask is None:
        change_point_probs_prior = torch.ones(n_iter)
    elif mask.any():
        change_point_probs_prior = mask.float()
    else:
        return n_iter-1
    change_point = pyro.sample('change_point_{}'.format(piece), dist.Categorical(probs=change_point_probs_prior),infer={'enumerate': 'parallel'})
    return change_point

def sample_linear_regression():
    slope = pyro.sample('slope', dist.Normal(0.,1.))
    intercept = pyro.sample('intercept', dist.Normal(0.,1.))
    noise_std = pyro.sample('noise_std', dist.LogNormal(0.,1.))
    return slope, intercept, noise_std

def sample_slope_and_noise_std(piece):
    slope = pyro.sample('slope_{}'.format(piece), dist.Normal(0.,1.))
    noise_std = pyro.sample('noise_std_{}'.format(piece), dist.LogNormal(0.,1.))
    return slope, noise_std

The guide has all the same distributions as the model: https://pastebin.com/sYmCpR6B

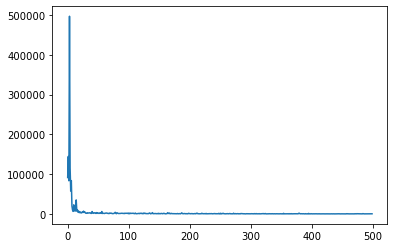
I want to enumerate the change points out with TraceEnum_ELBO, though it looks like that won’t scale very well with more change points. But even with just one change point, I don’t get a good fit, even though the elbo converges:

pyro.clear_param_store()
optim = pyro.optim.Adam({"lr": 0.05})
elbo = TraceEnum_ELBO(max_plate_nesting=1, num_particles=10)
svi = SVI(piecewise_regression, piecewise_regressionGuide, optim, loss=elbo)

losses = []
for i in range(500):
    losses.append(svi.step(x,y,2))

plt.plot(losses)

elbo

pred = pyro.infer.predictive.Predictive(pyro.poutine.uncondition(piecewise_regression),guide=piecewise_regressionGuide,num_samples=100)

fit = pred(x,y,2)

fit_obs_mean = fit['obs'].mean(0).detach().numpy()
fit_obs_std = fit['obs'].std(0).detach().numpy()

%matplotlib inline
plt.plot(x,y)
#plt.plot(x,slope_fit*x.numpy()+intercept_fit)
#plt.plot(x,fit_obs)
plt.errorbar(x,fit_obs_mean,yerr=fit_obs_std)
plt.axis('equal');

fit

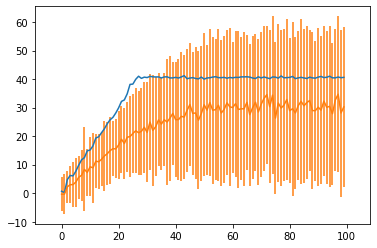
What can I do to make the fit more accurate? Is there a better way to implement this model? I’ve tried having Dirichlet priors on the change points, and multiple restarts (which helps a little, but best of 10 restarts still isn’t great).
Thanks

2

Hi @deoxy,
I’m not sure why your discrete model fails to converge, but I would guess a continuous parameterization would converge faster and more reliably, and would additionally scale to multiple pieces. Here’s an attempt at a continuous parameterization:

def piecewise_eval(knot_x, knot_y, x):
    # I haven't unit tested this:
    n_knots = knot_x.size(-1)
    assert n_knots >= 2
    knot_x, idx = knot_x.sort(dim=-1)
    knot_y = knot_y[..., idx] # this might not play well with batching
    lb = (x.unsqueeze(-1) > knot_x.unsqueeze(-2)).long().sum(-1)
    lb[lb >= knot_x.size - 1] = knot_x.size - 2
    ub = lb + 1
    x0 = knot_x[..., lb]
    x1 = knot_x[..., ub]
    y0 = knot_y[..., lb]
    y1 = knot_y[..., ub]
    return (y1 * (x - x0) + y0 * (x1 - x)) / (x1 - x0).clamp(min=1e-8)
    
def piecewise_regression(x, y, n_pieces=3):
    knot_x = pyro.sample("knot_x",
                         dist.Uniform(0, 100)
                             .expand([n_pieces]).to_event(n_pieces))
    knot_y = pyro.sample("knot_y",
                         dist.Normal(0, 100)
                             .expand([n_pieces]).to_event(n_pieces))
    y_pred = piecewise_eval(knot_x, knot_y, x)
    y_scale = pyro.sample("y_scale", dist.LogNormal(0, 5))
    pyro.sample("obs", dist.Normal(y_pred, y_scale),
                obs=y)

guide = AutoNormal(piecwise_regression)
3

Thanks for the answer @fritzo, I tried implementing your suggestion:

def piecewise_eval(knot_x, knot_y, x):
    # I haven't unit tested this:
    n_knots = knot_x.size(-1)
    assert n_knots >= 2
    knot_x, idx = knot_x.sort(dim=-1)
    knot_y = knot_y.gather(-1,idx)
    lb = (x.unsqueeze(-1) > knot_x[...,1:].unsqueeze(-2)).long().sum(-1)
    lb[lb >= n_knots - 1] = n_knots - 2
    ub = lb + 1
    x0 = knot_x.gather(-1,lb)
    x1 = knot_x.gather(-1,ub)
    y0 = knot_y.gather(-1,lb)
    y1 = knot_y.gather(-1,ub)
    slopes = (y1-y0)/(x1-x0).clamp(min=1e-8)
    return slopes*x + (y1 - slopes*x1)
    
def piecewise_regression(x, y, n_pieces=3):
    knot_x = pyro.sample("knot_x",
                         dist.Uniform(0, 100)
                             .expand([n_pieces]).to_event(0))
    knot_y = pyro.sample("knot_y",
                         dist.Normal(0, 100)
                             .expand([n_pieces]).to_event(0))
    y_pred = piecewise_eval(knot_x, knot_y, x)
    y_scale = pyro.sample("y_scale", dist.LogNormal(0, 1))
    y = pyro.sample("obs", dist.Normal(y_pred, y_scale),
                obs=y)
    return y

and train with an AutoDiagonalNormal guide. It seems like the parameters basically remain close to the initialization, no matter the learning rate and number of iterations (see notebook).
I know it’s not a lot to go on, but any ideas on what I could do to make it work?

4

is that clamp what you want? maybe it’s blocking all gradient flow?

5

I tried removing the clamp, but with or without it the gradient norms are big:
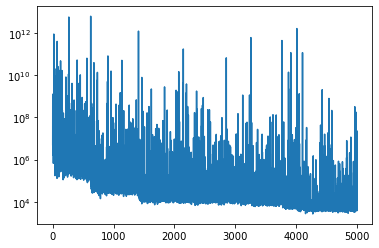image (that’s the AutoDiagonalNormal loc gradient)
I did get a good fit once with a different version of the model and a custom guide, which I’m guessing was due to a lucky initialization, on n_pieces = 2 (i.e. just regular linear regression) data. It’s strange if a different parametrization should make it that much harder.

6

I changed the model so that the knot parameters are sampled from U(0,1) and N(0,1) and then scaled by the length of x, and it works now. I updated the notebook above in case anyone is interested. Thanks for the help @fritzo, @martinjankowiak!

1 Like
7

Nice notebook @deoxy! If you ever feel like turning that into a tutorial we’d be happy to host that at Getting Started With Pyro: Tutorials, How-to Guides and Examples — Pyro Tutorials 1.8.4 documentation, and I’d be happy to review :slightly_smiling_face:

Also note that ClippedAdam might help with those large gradient norms.

1 Like