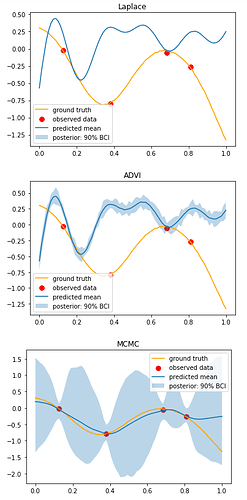
Hi, I am comparing inference results on the same data using the three aforementioned methods. Results produced by NUTS look very sensible, while Laplace and MultivariateNormal approximations produce not very meaningful results. Am I not using the SVI call properly? I have experimented with different step sizes for optimisation, and tried different optimisers too - Adam, Adagrad, RMSProp, SGD, and still no luck.
graphical comparison of results:
notebook:
variational inference is an approximation—and not necessarily a very good one. in the present case you’re doing inference over a relatively high-dimensional latent variable (the function values) that are highly correlated. to get sensible results you need to take especial care with the optimization, and even in that case you will likely underperform mcmc. for example one thing that would probably help is to reparameterize the function values in terms of whitened variables that are governed by a fixed N(0, 1) prior.
1 Like
thank you @martinjankowiak. I assume you were talking about the Cholesky decomposition? I have reparametrized the model. Laplace inference indeed looks better - at least, the mean curve is fitted well.
However, in this reparameterisation NUTS runs longer and does not converge as well as in the original model. Why could this be?
updated notebook: 063_1dGP_NUTS_Laplace_ADVI_n80_Cholesky.ipynb - Google Drive
can i ask what your goal is? normally the function values are integrated out if doing so is feasible, as is done here
I am interested in estimating the noise free function f (i.e. to denoising y), and to compare how the three different inference methods - NUTS, Laplace, ADVI - perform at this task