NUTS speed and chain behavior (Numpyro)

numpyro
1

Hello,

I am curious to see if the training time for my model is what would be expected for this kind of model.

The model is a fairly simple linear mixed effect model with parameters (and shapes) a (118), c (83 x 118), B (6 x 118), d (809 x 118), E(83 x 118), f(118).

So the total number of parameters is around 116,000.

The model has 2 levels

y_zyx ~ N(a_x + c_zx + X^T*B_x + d_yx, E_zx)
E_zx ~ IG(2, f_x)
Then there are defined priors for a,c,B,d,f

with 3309 observations (3309 observations x 118 features)

The training time is approximately 14 hours using 4 GPU in parallel (4 chains, 10,000 samples). I am also using plate.

A similar model (approximately same number of levels but single-level) took around 8 hours under the same settings.

Also:
While some of the parameters have fairly stable chain behavior:
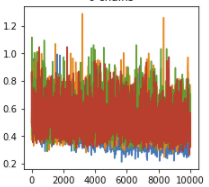
image

Others look more unstable:
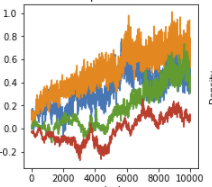
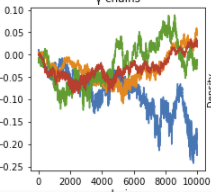
image
image

Is this expected from NUTS, or is it an indicator that I need to take more samples?

In summary, I am wondering a) if a 14 hour training time (4 gpu, parallel) for a 116,000 parameter model (4 chains, 10,000 samples, 1,000 warmup) and b) if the sampling behavior is familiar

Thanks!

2

it’s hard to say without more details but 116k is a very high dimension. inference in this regime is almost always hard and is expected to take significant computational resources. this is especially the case if the geometry of the posterior is such that the NUTS tree recursion (controlled by max_tree_depth) needs to go deep in most steps.

the trace plots for the parameters you labeled as “unstable” have high autocorrelation and make it clear that MCMC is not converging. you either need more samples, more max_tree_depth, a change in geometry (reparameterization), etc. to improve results. that said, you don’t necessarily need perfectly converged MCMC chains if all you care about is e.g. prediction, but you do want converged MCMC chains if you care about the details of the posterior.

1 Like