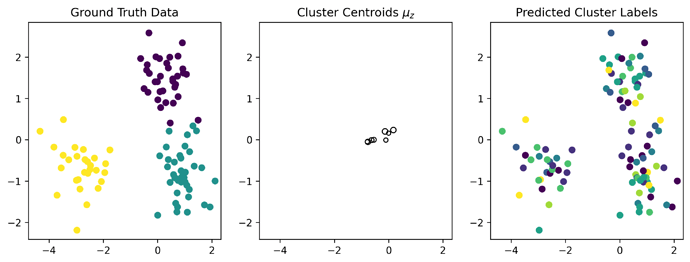
I’m attempting to adapt the Pyro DPGMM tutorial (Dirichlet Process Mixture Models in Pyro — Pyro Tutorials 1.8.4 documentation) to NumPyro but I’m getting very poor results with simple data:
How does one go about debugging why this is happening? I consistently find that the clusters’ means are too close together and tightly packed around 0, even though the means are drawn from N(0, 6*Identity), which is puzzling. This is with 50k optimization steps.
Snippets of my code are below (sorry about the indentation):
def model(obs):
with numpyro.plate('beta_plate', truncation_num_clusters - 1):
beta = numpyro.sample(
'beta',
numpyro.distributions.Beta(1, concentration_param))
with numpyro.plate('mean_plate', truncation_num_clusters):
mean = numpyro.sample(
'mean',
numpyro.distributions.MultivariateNormal(
jnp.zeros(obs_dim),
6.0 * jnp.eye(obs_dim)))
with numpyro.plate('data', num_obs):
z = numpyro.sample(
'z',
numpyro.distributions.Categorical(mix_weights(beta=beta)))
numpyro.sample(
'obs',
numpyro.distributions.MultivariateNormal(
mean[z],
0.3 * jnp.eye(obs_dim)),
obs=obs)
def guide(obs):
q_beta_params = numpyro.param(
'q_beta_params',
init_value=jax.random.uniform(
key=jax.random.PRNGKey(0),
minval=0,
maxval=2,
shape=(truncation_num_clusters - 1,)),
constraint=numpyro.distributions.constraints.positive)
with numpyro.plate('beta_plate', truncation_num_clusters - 1):
q_beta = numpyro.sample(
'beta',
numpyro.distributions.Beta(
concentration0=jnp.ones(truncation_num_clusters - 1),
concentration1=q_beta_params))
q_means_params = numpyro.param(
'q_means_params',
init_value=jax.random.multivariate_normal(
key=jax.random.PRNGKey(0),
mean=jnp.zeros(obs_dim),
cov=model_params['gaussian_mean_prior_cov_scaling'] * jnp.eye(obs_dim),
shape=(truncation_num_clusters, )))
with numpyro.plate('mean_plate', truncation_num_clusters):
q_mean = numpyro.sample(
'mean',
numpyro.distributions.MultivariateNormal(
q_means_params,
model_params['gaussian_cov_scaling'] * jnp.eye(obs_dim)))
q_z_assignment_params = numpyro.param(
'q_z_assignment_params',
init_value=jax.random.dirichlet(key=jax.random.PRNGKey(0),
alpha=jnp.ones(
truncation_num_clusters) / truncation_num_clusters,
shape=(num_obs,)),
constraint=numpyro.distributions.constraints.simplex)
with numpyro.plate('data', num_obs):
q_z = numpyro.sample(
'z',
numpyro.distributions.Categorical(probs=q_z_assignment_params))
optimizer = numpyro.optim.Adam(step_size=learning_rate)
svi = numpyro.infer.SVI(model,
guide,
optimizer,
loss=numpyro.infer.Trace_ELBO())
svi_result = svi.run(jax.random.PRNGKey(0),
num_steps=num_steps,
obs=observations,
progress_bar=True)