Multivariate Regression with Identity Covariance Matrix Producing Unexpected Correlated Output

1

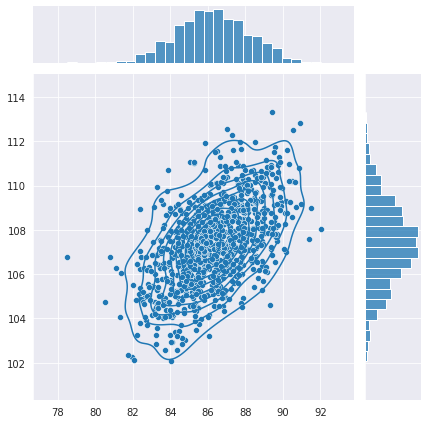
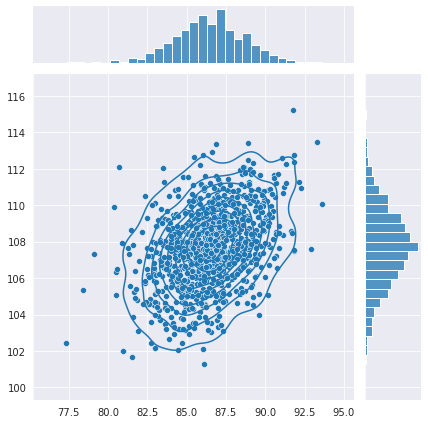
So, I am trying to create two regression models for multivariate outputs (2 outputs to be exact). The first model will explicitly infer the correlation while the second model I am specifying identity covariance matrix which I assumed would make the model act as if it is really just doing two independent linear regressions. Here is the code for the first model:

def model(x, y=None):
    β = pyro.sample("β", dist.Normal(torch.zeros(x.shape[1],2),torch.ones(x.shape[1],2)).to_event(2))
    B0 = pyro.sample("B0", dist.Normal(torch.zeros(2,),torch.ones(2,)))
    μ = torch.matmul(x,β) +  B0
    θ = pyro.sample("θ", dist.HalfNormal(torch.ones(2)))
    η = pyro.sample("η", dist.HalfNormal(1.))
    L = pyro.sample("L", dist.LKJCorrCholesky(2, η))
    L_Ω = torch.mm(torch.diag(θ.sqrt()), L)
    with pyro.plate("data", x.shape[0]):
        obs = pyro.sample("obs", dist.MultivariateNormal(loc=μ, scale_tril=L_Ω), obs=y)

And for the second model:

def model_no_cov(x, y=None):
    β = pyro.sample("β", dist.Normal(torch.zeros(x.shape[1],2),torch.ones(x.shape[1],2)).to_event(2))
    B0 = pyro.sample("B0", dist.Normal(torch.zeros(2,),torch.ones(2,)))
    μ = torch.matmul(x,β) +  B0
    with pyro.plate("data", x.shape[0]):
        obs = pyro.sample("obs", dist.MultivariateNormal(loc=μ, covariance_matrix=torch.eye(2)), obs=y)

What’s really driving me crazy is that the second model is producing outputs that are even more correlated than the actual data which you can see here:

download
download710×264 22.5 KB

I also should point out the second model has lower prediction error on the test set than the first model, which sort of boggles my mind. I’m not sure if I’m doing something wrong or my model just doesn’t make sense.

2

Hi @thecity2. What are your predictions? Are these posterior samples from MCMC or from SVI? Or are the samples from your prior? Note an uncorrelated prior does not imply an uncorrelated posterior.

3

@fritzo I’ve used both the SVI and mcmc now. Similar results (better accuracy with mcmc though). The samples I’m showing in the above plot on the left are from SVI. I guess my question about it is whether there’s a way to “fix” the correlation such that it is diagonal. Starting to think maybe not.

4

Thinking more about this…I showed the means being highly correlated, but the distributions for each individual sample have quite a lot of variance. I suppose this makes more sense now. Here’s an example of the joint for one test sample using the covariance model. download

Here’s the same sample predicted by the second model (it seems less correlated to my eyes):
download (3)

5

Again it helps to be clear about whether you’re interested in “prior correlation” or “posterior correlation”. Let’s assume you mean “posterior correlation”. While it is rare to know anything about posterior correlation structure, in some cases you may know for physical reasons that the posterior should be uncorrelated. In that case you could specify a variational distribution (a guide) with diagonal posterior.

def model_no_cov():  # prior excludes off-diagonal terms
    β = pyro.sample("β", dist.Normal(torch.zeros(x.shape[1],2),torch.ones(x.shape[1],2)).to_event(2))
    B0 = pyro.sample("B0", dist.Normal(torch.zeros(2,),torch.ones(2,)))
    μ = torch.matmul(x,β) +  B0
    with pyro.plate("data", x.shape[0]):
        obs = pyro.sample("obs", dist.Normal(μ, 1).to_event(1), obs=y)

# here are two possible variational families
guide_no_cov = AutoNormal(model_no_cov)  # excludes off-diagonal terms
guide_w_cov = AutoMultivariateNormal(model_no_cov)  # allows off-diagonal terms

(Also note that if neither your model nor guide allow off-diagonal covariance terms, you can simply use Normal(loc,scale).to_event(1) instead of MultivariateNormal(loc,torch.diag_embed(scale**2)).)

6

Thanks @fritzo, actually, your last point about using Normal makes sense. I will try that.